Двигатель не двигает корабль.
Корабль остается на месте, а
двигатели двигают вселенную
вокруг него.

Футурама

Это один из самых важных уроков. Вдумчиво прочитайте его хотя бы восемь раз.

Гомогенные координаты

В предыдущих уроках мы предполагали, что вершина расположена по координатам (x, y, z). Давайте-ка добавим еще одну координату – w. Отныне вершины у нас будут по координатам (x, y, z, w)

Вскоре вы поймете, что к чему, но пока примите это как данность:

• Если w==1, тогда вектор (x,y,z,1) – это позиция в пространстве
• Если w==0, тогда вектор (x,y,z,0) – это направление.

Запомните это как аксиому без доказательств!!!

И что это нам дает? Ну, для вращения ничего. Если вы вращаете точку или направление, то получите один и тот же результат. Но если вы вращаете перемещение(когда вы двигаете точку в определенном направлении), то все кардинально меняется. А что значит «переместить направление»? Ничего особенного.

Гомогенные координаты позволяют нам оперировать единым матаппаратом для обоих случаев.

Матрицы Трансформаций

Введение в матрицы

Если по простому, то матрица, это просто массив чисел с фиксированным количеством строк и столбцов.

Например, матрица 2 на 3 будет выглядеть так:

В 3д графике мы пользуемся почти всегда матрицами 4х4. Это позволяет нам трансформировать наши (x,y,z,w) вершины. Это очень просто – мы умножаем вектор позиции на матрицу трансформации.

Матрица*Вершину = трансформированная вершина

Все не так страшно как выглядит. Укажите пальцем левой руки на a, а пальцем правой руки на x. Это будет ax. Переместите левый палец на следующее число b, а правый палец вниз на следующее число – y. У нас получилось by. Еще раз – cz. И еще раз – dw. Теперь суммируем все получившиеся числа – ax+by +cz +dw . Мы получили наш новый x. Повторите то же самое для каждой строки и вы получите новый вектор (x,y,z,w).

Однако это довольно скучная операция, так что пусть её за нас будет выполнять компьютер.

В С++ при помощи библиотеки GLM:

glm::mat4 myMatrix;

glm::vec4 myVector;

glm :: vec 4 transformedVector = myMatrix * myVector ; // Не забываем про порядок!!! Это архиважно!!!

В GLSL:

mat4 myMatrix;

vec4 myVector;

// заполняем матрицу и вектор нашими значениями… это мы пропускаем

vec 4 transformedVector = myMatrix * myVector ; // точно так же как и в GLM

(Чего-то мне кажется, что вы не скопировали этот кусок кода к себе в проект и не попробовали…ну же, попробуйте, это интересно!)

Матрица перемещений

Матрица перемещения, это, наверное, самая простая матрица из всех. Вот она:

Тут X, Y, Z – это значения, которые мы хотим добавить к нашей позиции вершины.

Итак, если нам нужно переместить вектор (10,10,10,1) на 10 пунктов, по позиции Х, то:
(Попробуйте это сами, ну пожаааалуйста!)

…И у нас получится (20,10,10,1) в гомогенном векторе. Как вы, я надеюсь, помните, 1 значит, что вектор представляет собой позицию, а не направление.

А теперь давайте попробуем таким же образом трансформировать направление (0,0,-1,0):

И в итоге у нас получился тот же вектор (0,0,-1,0).
Как я и говорил, двигать направление не имеет смысла.

Как же нам закодить это?

В С++ при помощи GLM:

#include // после

glm::mat4 myMatrix = glm::translate(10.0f, 0.0f, 0.0f );

glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f );

glm :: vec 4 transformedVector = myMatrix * myVector ; // и какой у нас получится результат?

А в GLSL: В GLSL так редко кто делает. Чаще всего с помощью функции glm::translate(). Сначала создают матрицу в С++, а затем отправляют её в GLSL, и уже там делают лишь одно умножение:

vec4 transformedVector = myMatrix * myVector;

Единичная матрица(Identity Matrix)

Это специальная матрица. Она не делает ничего. Но я упоминаю её, так как важно знать, что умножение A на 1.0 в результате дает А:

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Матрица Масштабирования

Матрица масштабирования так же достаточно проста:

Поэтому если вам хочется увеличить вектор(позицию или направление, не важно) в два раза по всем направлениям:

А координата w не поменялась. Если вы спросите: «А что такое масштабирование направления?». Полезно не часто, но иногда полезно.

(заметьте, что масштабирование единичной матрицы с (x,y,z) = (1,1,1))

С++:

// Используйте #include и #include

glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Матрица Вращения

А вот эта матрица достаточно сложная. Поэтому я не буду останавливаться на подробностях её внутренней реализации. Если сильно хочется, лучше почитайте (Matrices and Quaternions FAQ)

В С ++:

// Используйте #include и #include

glm::vec3 myRotationAxis(??, ??, ??);

glm::rotate(angle_in_degrees, myRotationAxis);

Совмещенные Трансформации

Теперь мы знаем как вращать, перемещать и масштабировать наши вектора. Хорошо бы узнать, как объединить все это. Это делается просто умножением матриц друг на друга.

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

И снова порядок!!! Сначала нужно изменить размер, потом прокрутить и лишь потом сдвинуть.

Если мы будем применять трансформации в другом порядке, то не получим такой же результат. Вот попробуйте:

• Сделайте шаг вперед(не свалите компьютер со стола) и повернитесь влево
• Повернитесь влево и сделайте один шаг вперед.

Да, нужно всегда помнить про порядок действий при управлении, например, игровым персонажем. Сначала, если нужно, делаем масштабирование, потом выставьте направление(вращение) а потом перемещайте. Давайте разберем небольшой пример(я убрал вращение для облегчения расчетов):

Не правильный способ:

• Перемещаем корабль на (10,0,0). Его центр теперь на 10 по Х от центра.
• Увеличиваем размер нашего корабля в 2 раза. Каждая координата умножается на 2 относительно центра который далеко… И в итоге у нас получается корабль необходимого размера но по позиции 2*10=20. Что не совсем то, чего мы хотели.

Правильный способ:

• Увеличиваем размер корабля в 2 раза. Теперь у нас есть большой корабль расположенный по центру.
• Перемещаем корабль. Размер корабля не изменился и он расположен в нужном месте.

Умножение матрицы на матрицу выполняется почти так же, как и умножение матрицы на вектор. Не будем вдаваться в подробности, а любопытствующие пусть почитают это из специализированных источников. Мы же просто будем полагаться на библиотеку GLM.
ВС++:
glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;
В GLSL:
mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Матрицы Модели, Вида и Проекции

Для иллюстраций предполагаем, что мы уже умеем рисовать в OpenGL любимую 3д модель программы Blender – голову обезьяны Сюзанны.

Матрицы Модели, Вида и Проекции очень удобный метод разделения трансформаций. Если сильно хочется, вы можете не использовать их(мы же не использовали их в уроках 1 и 2). Но я настойчиво рекомендую вам пользоваться ими. Просто почти все 3д библиотеки, игры итд используют их для разделения трансформаций.

Матрица Модели

Данная модель, как и наш любимый треугольничек, задана набором вершин. X, Y, Z координаты заданы относительно центра объекта. Так вот, если вершина расположена по координатам (0,0,0), то она находится в центре всего объекта

Теперь мы имеем возможность двигать нашу модель. Например, потому, что пользователь управляет ей с помощью клавиатуры и мыши. Это сделать очень просто: масштабирование*вращение*перемещение и все. Вы применяете вашу матрицу ко всем вершинам в каждом кадре(в GLSL а не в C++) и все перемещается. Все что не перемещается – расположено в центре «мира».

Вершины находятся в мировом пространстве Черная стрелка на рисунке показывает, как мы переходим из пространства модели, в мировое пространство(Все вершины были заданы относительно центра модели, а стали заданы относительно центра мира)

Эту трансформацию можно отобразить следующей диаграммой:

Матрица Вида

Давайте еще раз прочитаем цитату из футурамы:

«Двигатель не двигает корабль. Корабль остается на месте, а двигатели двигают вселенную вокруг него.»

То же самое можно применить и к фотоаппарату. Если вы хотите сфотографировать гору под каким-нибудь углом, то можно передвинуть фотокамеру…или гору. В реальной жизни это невозможно, но очень легко и удобно в компьютерной графике.

По умолчанию наша камера находится в центре Мировых Координат. Чтобы двигать наш мир нужно создать новую матрицу. К примеру нам нужно переместить нашу камеру на 3 единицы вправо(+Х). Это то же самое, что переместить весь мир на 3 единицы влево(-Х). И пока ваши мозги плавятся, давайте попробуем:

// Используйте #include и #include

glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);

Картинка ниже демонстрирует это: мы переходим от Мирового пространства(все вершины заданы относительно центра мира как мы это делали в предыдущей секции) к пространству камеры(все вершины заданы относительно камеры).

И прежде чем ваша голова совсем взорвется, посмотрите на прекрасную функцию из нашей старой доброй GLM:

glm::mat4 CameraMatrix = glm::LookAt(

cameraPosition , // Позиция камеры в мировых координатах

cameraTarget , // точка на которую мы хотим посмотреть в мировых координатах

upVector // скорее всего glm :: vec 3(0,1,0), а (0,-1,0) будет все показывать вверх ногами, что иногда тоже прикольно.

Вот иллюстрация к вышесказанному:

Но к нашей радости, это еще не все.

Матрица Проекции

Сейчас мы имеем координаты в пространстве камеры. Это значит, что после всех этих трансформаций, вершина которой посчастливилось оказаться в x==0 и y==0 будет отрендерена в центре экрана. Но мы же не можем пользоваться лишь координатами X,Y, чтобы понять куда рисовать вершину: дистанция к камере(Z) должна тоже учитываться! Если у нас есть две вершины, то одна из них будет более ближе к центру экрана чем другая, так как у неё больше координата Z.

Это называется перспективная проекция:

И к большому счастью для нас, матрица 4х4 может представлять собой и перспективные трансформации:

glm::mat4 projectionMatrix = glm::perspective(

FoV , // Горизонтальное Поле Вида в градусах. Или величина приближения . Как будто « линза » на камере . Обычно между 90(суперширокий, как рыбий глаз) и 30(как небольшая подзорная труба)

4.0 f / 3.0 f , // Соотношение сторон. Зависит от размера вашего окна. Например, 4/3 == 800/600 == 1280/960, знакомо, не правда ли?

0.1 f , // Ближнее поле отсечения. Его нужно задавать как можно большим, иначе будут проблемы с точностью.

100.0 f // Дальнее поле отсечения. Нужно держать как можно меньшим.

);

Повторим то что мы сейчас сделали:

Мы ушли от пространства камеры(все вершины заданы в координатах относительно камеры) в гомогенное пространство(все вершины в координатах маленького куба(-1,1). Все что находится в кубе – находится на экране.)

И финальная диаграмма:

Вот еще одна картинка чтобы стало яснее, что же происходит, когда мы умножаем всю эту проекционную матричную ерунду. Перед умножением на проекционную матрицу у нас есть голубые объекты заданные в пространстве камеры и красный объект, который представляет собой поле вида камеры: пространство которое попадает в объектив камеры:

После умножения на проекционную матрицу у нас выходит следующее:

На предыдущей картинке поле вида превратилось в идеальный куб(с координатами вершин от -1 до 1 по всем осям.), а все объекты деформированы в перспективе. Все голубые объекты которые близко к камере – стали большими, а которые дальше – маленькими. Так же как и в жизни!

Вот какой вид у нас открывается из «объектива»:

Однако оно квадратное, и нужно применить еще одно математическое преобразование, чтобы подогнать картинку под размеры окна.

В компьютерной графике определенны понятия различных матриц. Это мировая матрица (World Matrix), матрица вида (View Matrix) и матрица проекции (Projection Matrix). С помощью данных матриц в исходном коде программы производятся матричные преобразования над моделями. Матричные преобразования подразумевают под собой умножение каждой вершины объекта на одну из матриц, а точнее последовательное умножение всех вершин объекта на каждую из трех матриц. Такой подход позволяет корректно представить модель в трехмерном пространстве вашего двухмерного монитора. Техника прохода модели через три перечисленные матрицы представляет суть механизма работы с графическими данными в трехмерной плоскости монитора.

Мировая матрица

Мировая матрица – позволяет производить различные матричные преобразования (трансформацию и масштабирование) объекта в мировой системе координат. Мировая система координат – это своя локальная система координат данного объекта, которой наделяется каждый объект, скажем так прошедший через мировую матрицу, поскольку каждая вершина участвует в произведении этой матрицы.

Новая локальная система координат значительно упрощает аффинные преобразования объекта в пространстве. Например, чтобы перенести объект с левого верхнего угла дисплея в нижний правый угол дисплея, то есть переместить игровой объект в пространстве, необходимо просто перенести его локальную точку отсчета, системы координат на новое место. Если бы не было мировой матрицы, то этот объект пришлось переносить по одной вершине. Поэтому любой объект, а точнее все вершины этого объекта проходят через мировую матрицу преобразования.

Как уже упоминалось, мировое преобразование вершин объекта может состоять из любых комбинаций вращения, трансляции и масштабирования. В математической записи вращение вершины по оси Х выглядит следующим образом:

Мировая матрица

где cos - угол вращения в радианах.

Вращение вершины вокруг оси Y выглядит так:

Вращение вершины вокруг оси Y

А вращение вокруг оси Z происходит по следующей формуле:

вращение вокруг оси Z

Трансляция вершины позволяет переместить эту саму вершину с координатами x, y, z в новую точку с новыми координатами x1, y1, z1. В математической записи это выглядит так:

X1 = x + Tx y1 = y + Ty z1 = z + Tz

Трансляция вершины в матричной записи выглядит следующим образом:

Трансляция вершины в матричной записи

где Tx, Ty и Tz - значения смещения по осям X, Y и Z.

Масштабировать вершину в пространстве (удалять или приближать) с координатами x, y, z в новую точку с новыми значениями x1, y1, z1, можно посредством следующей записи:

X1 = x * S y1 = y * S z1 = z * S

В матричной записи это выражается следующим образом:

Масштабировать вершину

где Sx, Sy, Sz - значения коэффициентов растяжения или сжатия по осям X, Y, Z.

Все перечисленные операции можно делать в исходном коде программы вручную, то есть вычислять приведенные записи так, как я их только что описал. Но естественно так никто не делает (почти никто), потому что в DirectX имеется огромное количество методов, которые сделают все выше приведенные операции за вас.

Матрица вида

Матрица вида – задает местоположение камеры в пространстве и это вторая по счету матрица, на которую умножаются вершины объекта. Эта матрица способствует определению направления просмотра трехмерной сцены. Трехмерная сцена – это все то, что вы видите на экране монитора. Это как в театре, где вы сидите в портере или на галерке и наблюдаете за действиями на сцене. Так вот сидя в портере у вас будет одно местоположение камеры, а сидя на галерке уже совсем другое.

Фактически эта матрица позволяет определять жанр игры. Например, игра DOOM от первого лица – это можно сказать первые ряды портера в театре, тогда как игра Warcraft – это галерка на балконе. Матрица вида предназначена для определения положения камеры в пространстве, и вы можете смещать позицию камеры влево, вправо, вверх, вниз, удалять, приближать ее и так далее.

Матрица проекции

Матрица проекции – это более сложная матрица, которая создает проекцию трехмерного объекта на плоскость двумерного экрана монитора. С помощью этой матрицы определяются передняя и задняя области отсечения трехмерного пространства, что позволяет регулировать пространство отсечения невидимых на экране объектов, а заодно и снизить нагрузку процессора видеокарты. На рисунке изображен механизм проекции объекта в плоскости и отсечение пространства.

Матрица проекции

В определённый момент у любого разработчика в области компьютерной графики возникает вопрос: как же работают эти перспективные матрицы? Подчас ответ найти очень непросто и, как это обычно бывает, основная масса разработчиков бросает это занятие на полпути.

Это не решение проблемы! Давайте разбираться вместе!

Будем реалистами с практическим уклоном и возьмём в качестве подопытного OpenGL версии 3.3. Начиная с этой версии каждый разработчик обязан самостоятельно реализовывать модуль матричных операций. Замечательно, это то, что нам нужно. Проведём декомпозицию нашей с вами нелёгкой задачи и выделим основные моменты. Немного фактов из спецификации OpenGL:

• Матрицы хранятся по столбцам (column-major);
• Однородные координаты;
• Канонический объём отсечения (CVV) в левосторонней системе координат.

Существует два способа хранения матриц: сolumn-major и row-major. На лекциях по линейной алгебре как раз используется схема row-major. По большому счёту представление матриц в памяти не имеет значения, потому что матрицу всегда можно перевести в одного вида представления в другое простым транспонированием. А раз разницы нет, то для всех последующих расчётов мы будем использовать классические row-major матрицы. При программировании OpenGL есть небольшая хитрость, которая позволяет отказаться и от транспонирования матриц при сохранении классических row-major расчётов. В шейдерную программу матрицу нужно передавать как есть, а в шейдере производить умножение не вектора на матрицу, а матрицы на вектор.

Однородные координаты – это не очень хитрая система с рядом простых правил по переводу привычных декартовых координат в однородные координаты и обратно. Однородная координата это матрица-строка размерности . Для того чтобы перевести декартову координату в однородную координату необходимо x , y и z умножить на любое действительное число w (кроме 0). Далее необходимо записать результат в первые три компоненты, а последний компонент будет равен множителю w . Другими словами:
- декартовы координаты
w – действительное число, не равное 0

- однородные координаты

Небольшой трюк: Если w равно единице, то всё что нужно для перевода, это перенести компоненты x , y и z и приписать единицу в последний компонент. То есть получить матрицу-строку:

Несколько слов о нуле в качестве w . С точки зрения однородных координат это вполне допустимо. Однородные координаты позволяют различать точки и вектора. В декартовой же системе координат такое разделение невозможно.

- точка, где (x, y, z ) – декартовы координаты

- вектор, где (x, y, z ) – радиус-вектор

Обратный перевод вершины из однородных координат в декартовы координаты осуществляется следующим образом. Все компоненты матрицы-строки необходимо разделить на последнюю компоненту. Другими словами:

- однородные координаты
- декартовы координаты

Главное что необходимо знать, что все алгоритмы OpenGL по отсечению и растеризации работают в декартовых координатах, но перед этим все преобразования производятся в однородных координатах. Переход от однородных координат в декартовы координаты осуществляется аппаратно.

Канонический объём отсечения или Canonic view volume (CVV) – это одна из мало документированных частей OpenGL. Как видно из рис. 1 CVV – это выровненный по осям куб с центром в начале координат и длиной ребра равной двойке. Всё, что попадает в область CVV подлежит растеризации, всё, что находится вне CVV игнорируется. Всё, что частично выходит за границы CVV, подлежит алгоритмам отсечения. Самое главное что надо знать - система координат CVV левосторонняя!

Рис. 1. Канонический объём отсечения OpenGL (CVV)

Левосторонняя система координат? Как же так, ведь в спецификации к OpenGL 1.0 ясно написано, что используемая система координат правосторонняя? Давайте разбираться.

Рис. 2. Системы координат

Как видно из рис. 2 системы координат различаются лишь направлением оси Z . В OpenGL 1.0 действительно используется правосторонняя пользовательская система координат. Но система координат CVV и пользовательская система координат это две совершенно разные вещи. Более того, начиная с версии 3.3, больше не существует такого понятия как стандартная система координат OpenGL. Как упоминалось ранее, программист сам реализует модуль матричных операций. Формирование матриц вращения, формирование проекционных матриц, поиск обратной матрицы, умножение матриц – это минимальный набор операций, входящих в модуль матричных операций. Возникает два логичных вопроса. Если объём видимости это куб с длиной ребра равной двум, то почему сцена размером в несколько тысяч условных единиц видна на экране? В какой момент происходит перевод пользовательской системы координат в систему координат CVV. Проекционные матрицы – это как раз та сущность, которая занимается решением этих вопросов.

Главная мысль вышеизложенного – разработчик сам волен выбрать тип пользовательской системы координат и должен корректно описать проекционные матрицы. На этом с фактами об OpenGL закончено и подошло время сводить всё воедино.

Одна из наиболее распространённых и сложно постигаемых матриц – это матрица перспективного преобразования. Так как же она связана с CVV и пользовательской системой координат? Почему объекты с увеличением расстояния до наблюдателя становятся меньше? Для того чтобы понять почему объекты уменьшаются с увеличением расстояния, давайте рассмотрим матричные преобразования трёхмерной модели шаг за шагом. Не секрет, что любая трёхмерная модель состоит из конечного списка вершин, которые подвергаются матричным преобразованиям совершенно независимо друг от друга. Для того чтобы определить координату трёхмерной вершины на двухмерном экране монитора необходимо:

1. Перевести декартову координату в однородную координату;
2. Умножить однородную координату на модельную матрицу;
3. Результат умножить на видовую матрицу;
4. Результат умножить на проекционную матрицу;
5. Результат перевести из однородных координат в декартовы координаты.

Перевод декартовой координаты в однородную координату обсуждался ранее. Геометрический смысл модельной матрицы заключается в том, чтобы перевести модель из локальной системы координат в глобальную систему координат. Или как говорят, вынести вершины из модельного пространства в мировое пространство. Скажем проще, загруженный из файла трёхмерный объект находится в модельном пространстве, где координаты отсчитываются относительно самого объекта. Далее с помощью модельной матрицы производится позиционирование, масштабирование и поворот модели. В результате все вершины трёхмерной модели получают фактические однородные координаты в трёхмерной сцене. Модельное пространство относительно мирового пространства является локальным. Из модельного пространства координаты выносятся в мировое пространство (из локального в глобальное). Для этого используется модельная матрица.

Теперь переходим к шагу три. Здесь начинает работу видовое пространство. В этом пространстве координаты отсчитываются относительно положения и ориентации наблюдателя так, как если бы он являлся центром мира. Видовое пространство является локальным относительно мирового пространства, поэтому координаты в него надо вносить (а не выносить, как в предыдущем случае). Прямое матричное преобразование выносит координаты из некоторого пространства. Чтобы наоборот внести их в него, надо матричное преобразование инвертировать, поэтому видовое преобразование описывается обратной матрицей. Как же получить эту обратную матрицу? Для начала получим прямую матрицу наблюдателя. Чем характеризуется наблюдатель? Наблюдатель описывается координатой, в которой он находится, и векторами направления обзора. Наблюдатель всегда смотрит в направлении своей локальной оси Z . Наблюдатель может перемещаться по сцене и осуществлять повороты. Во многом это напоминает смысл модельной матрицы. По большому счёту так оно и есть. Однако, для наблюдателя операция масштабирования бессмысленна, поэтому между модельной матрицей наблюдателя и модельной матрицей трёхмерного объекта нельзя ставить знак равенства. Модельная матрица наблюдателя и есть искомая прямая матрица. Инвертировав эту матрицу, мы получаем видовую матрицу. На практике это означает, что все вершины в глобальных однородных координатах получат новые однородные координаты относительно наблюдателя. Соответственно, если наблюдатель видел определённую вершину, то значение однородной координаты z данной вершины в видовом пространстве точно будет положительным числом. Если вершина находилась за наблюдателем, то значение её однородной координаты z в видовом пространстве точно будет отрицательным числом.

Шаг четыре - это самый интересный шаг. Предыдущие шаги были рассмотрены так подробно намеренно, чтобы читатель имел полную картину о всех операндах четвёртого шага. На четвёртом шаге однородные координаты выносятся из видового пространства в пространство CVV. Ещё раз подчеркивается тот факт, что все потенциально видимые вершины будут иметь положительное значение однородной координаты z .

Рассмотрим матрицу вида:

И точку в однородном пространстве наблюдателя:

Произведём умножение однородной координаты на рассматриваемую матрицу:

Переведём получившиеся однородные координаты в декартовы координаты:

Допустим, есть две точки в видовом пространстве с одинаковыми координатами x и y , но разными координатами z . Другими словами одна из точек находится за другой. Из-за перспективного искажения наблюдатель должен увидеть обе точки. Действительно, из формулы видно, что из-за деления на координату z , происходит сжатие к точке начала координат. Чем больше значение z (чем дальше точка от наблюдателя), тем сильнее сжатие. Вот и объяснение эффекту перспективы.

В спецификации OpenGL сказано, что операции по отсечению и растеризации выполняются в декартовых координатах, а процесс перевода однородных координат в декартовы координаты производится автоматически.

Матрица (1) является шаблоном для матрицы перспективой проекции. Как было сказано ранее, задача матрицы проекции заключается в двух моментах: установка пользовательской системы координат (левосторонняя или правосторонняя), перенос объёма видимости наблюдателя в CVV. Выведем перспективную матрицу для левосторонней пользовательской системы координат.

Матрицу проекции можно описать с помощью четырёх параметров (рис. 3):

• Угол обзора в радианах (fovy );
• Соотношение сторон (aspect );
• Расстояние до ближней плоскости отсечения (n );
• Расстояние до дальней плоскости отсечения (f ).

Рис. 3. Перспективный объём видимости

Рассмотрим проекцию точки в пространстве наблюдателя на переднюю грань отсечения перспективного объёма видимости. Для большей наглядности на рис. 4 изображён вид сбоку. Так же следует учесть, что пользовательская система координат совпадает с системой координат CVV, то есть везде пользуется левосторонняя система координат.

Рис. 4. Проецирование произвольной точки

На основании свойств подобных треугольников справедливы следующие равенства:

Выразим yꞌ и xꞌ:

В принципе, выражений (2) достаточно для получения координат точек проекции. Однако для правильного экранирования трёхмерных объёктов необходимо знать глубину каждого фрагмента. Другими словами необходимо хранить значение компоненты z . Как раз это значение используется при тестах глубины OpenGL. На рис. 3 видно, что значение zꞌ не подходит в качестве глубины фрагмента, потому что все проекции точек умеют одинаковое значение zꞌ . Выход из сложившейся ситуации – использование так называемой псевдоглубины.

Свойства псевдоглубины:

1. Псевдоглубина рассчитывается на основании значения z ;
2. Чем ближе к наблюдателю находится точка, тем меньшеe значение имеет псевдоглубина;
3. У всех точек, лежащих на передней плоскости объёма видимости, значение псевдоглубины равно -1;
4. У всех точек, лежащих на дальней плоскости отсечения объёма видимости, значение псевдоглубины равно 1;
5. Все фрагменты, лежащие внутри объёма видимости, имеют значение псевдоглубины в диапазоне [-1 1].

Давайте выведем формулу, по которой будет рассчитываться псевдоглубина. В качестве основы возьмём следующее выражение:

Коэффициенты a и b необходимо вычислить. Для того чтобы это сделать, воспользуемся свойствами псевдоглубины 3 и 4. Получаем систему из двух уравнений с двумя неизвестными:

Произведём сложение обоих частей системы и умножим результат на произведение fn , при этом f и n не могут равняться нулю. Получаем:

Раскроем скобки и перегруппируем слагаемые так, чтобы слева осталась только часть с а , а справа только с b :

Подставим (6) в (5). Преобразуем выражение к простой дроби:

Умножим обе стороны на -2fn , при этом f и n не могут равняться нулю. Приведём подобные, перегруппируем слагаемые и выразим b :

Подставим (7) в (6) и выразим a :

Соответственно компоненты a и b равны:

Теперь подставим полученные коэффициенты в матрицу заготовку (1) и проследим, что будет происходить с координатой z для произвольной точки в однородном пространстве наблюдателя. Подстановка выполняется следующим образом:

Пусть расстояние до передней плоскости отсечения n равно 2, а расстояние до дальней плоскости отсечения f равно 10. Рассмотрим пять точек в однородном пространстве наблюдателя:

Взаимное расположение точки и объёма видимости

Точка	Значение	Описание
1	1	Точка находится перед передней плоскостью отсечения объёма видимости. Не проходит растеризацию.
2	2	Точка находится на передней грани отсечения объёма видимости. Проходит растеризацию.
3	5	Точка находится между передней гранью отсечения и дальней гранью отсечения объёма видимости. Проходит растеризацию.
4	10	Точка находится на дальней грани отсечения объёма видимости. Проходит растеризацию.
5	20	Точка находится за дальней гранью отсечения объёма видимости. Не проходит растеризацию.

Умножим все точки на матрицу (8), а затем переведём полученные однородные координаты в декартовые координаты . Для этого нам необходимо вычислить значения новых однородных компонент и .
Точка 1:

Обратите внимание, что однородная координата абсолютно верно позиционируется в CVV, а самое главное, что теперь возможна работа теста глубины OpenGL, потому что псевдоглубина полностью удовлетворяет требованиям тестов.

С координатой z разобрались, перейдём к координатам x и y . Как говорилось ранее весь перспективный объём видимости должен умещаться в CVV. Длина ребра CVV равна двум. Соответственно, высоту и ширину перспективного объёма видимости надо сжать до двух условных единиц.

В нашем распоряжении имеется угол fovy и величина aspect . Давайте выразим высоту и ширину, используя эти величины.

Рис. 5. Объём видимости

Из рис. 5 видно, что:

Теперь можно получить окончательный вид перспективной проекционной матрицы для пользовательской левосторонней системы координат, работающей с CVV OpenGL:

На этом вывод матриц закончен.

Пару слов о DirectX - основном конкуренте OpenGL. DirectX отличается от OpenGL только габаритами CVV и его позиционированием. В DirectX CVV - это прямоугольный параллелепипед с длинами по осям x и y равными двойке, а по оси z длина равна единице. Диапазон x и y равен [-1 1], а диапазон z равен . Что касается системы координат CVV, то в DirectX, как и в OpenGL, используется левосторонняя система координат.

Для вывода перспективных матриц для пользовательской правосторонней системы координат необходимо перерисовать рис. 2, рис.3 и рис.4 с учётом нового направления оси Z . Далее расчёты полностью аналогичны, с точностью до знака. Для матриц DirectX свойства псевдоглубины 3 и 4 модифицируются под диапазон .

На этом тему перспективных матриц можно считать закрытой.

Сегодня мы более подробно рассмотрим устройство виртуальной камеры. Начнём с картинки.

На рисунке мы видим координатное пространство камеры. Направление ("взгляд") камеры всегда совпадает с положительным направлением оси z, а сама камера расположена в начале координат.

Внутреннее пространство пирамиды изображённой на рисунке - это та часть виртуального мира, которую увидит пользователь.

Обратите внимание на три плоскости. Первая расположена на расстоянии 1 по оси z. Это ближняя плоскость. То что находится до неё игрок никогда не увидит. В данном случае значение z равно единице, но вообще говоря, оно может быть любым. Именно с ближней плоскостью связан один дефект отображения графики. Этот дефект проявляется прежде всего в шутерах (из-за большой свободы камеры). Когда ты слишком близко подходишь к объекту, то можно оказаться "внутри". Из последних игр этот дефект особенно сильно проявлялся в Left 4 dead: когда на игрока наваливалась толпа зомби, то очень часто можно было заглянуть внутрь других персонажей.

Плоскость расположенная на расстоянии 100 единиц по оси z называется дальней. Опять же, значение может быть произвольным. Пользователь никогда не увидит объекты расположенные дальше этой плоскости.

Шесть плоскостей ограничивающих пространство, которое увидит пользователь, называются отсекающими (clipping planes): левая правая верхняя нижняя ближняя и дальняя.

Плоскость расположенная между ближней и дальней - проекционная. В дальнейшем, эту плоскость мы будем располагать в z=1, т.е. она будет совпадать с ближней. Здесь я отделил ближнюю и проекционную плоскости, чтобы показать, что это всё-таки не одно и то же. Проекционная плоскость предназначена для последнего преобразования координат: преобразование из трёхмерного пространства камеры - в двухмерное пространство.

Именно благодаря проекционной плоскости пользователь увидит виртуальный мир. Собственно, эта плоскость и есть то, что увидит пользователь. Проекционная плоскость напрямую связана с такими понятиями как основной/фоновый буферы, окно программы и экран пользователя. Все эти понятия можно рассматривать как прямоугольную картинку, которая в памяти компьютера представлена массивом цифр.

Преобразование координат из трёхмерного мира в проекционную плоскость - самое сложное из тех, которые на данный момент были нами изучены.

Поле зрения/зона обзора (field of view)

На рисунке выше у проекционной плоскости (а значит и у изображения, которое увидит пользователь) ширина больше высоты. Ширина и высота проекционной плоскости задаются с помощью углов. Встречаются разные названия этих углов: поля зрения или зоны обзора. В английском - fields of view.

Зоны обзора задаются двумя углами. Назовём их: fovx - зона обзора по горизонтали, fovy - зона обзора по вертикали. Подробно о зонах обзора: ниже.

Z-буфер / w-буфер / буфер глубины (z-buffer / w-buffer / depth buffer)

Посмотрим на картинку, на которой представлено два треугольника: на расстоянии в 25 и 50 единиц от камеры. На рисунке (а) показано местоположение треугольников в пространстве (вид сверху), а на рисунке (б) можно увидеть конечное изображение:

Как вы возможно догадываетесь, изображение нужно рисовать начиная с самых дальных элементов и заканчивая самыми ближними. Очевидное решение: вычислить расстояние от начала координат (от камеры) до каждого объекта, а затем сравнить. В компьютерной графике используется немного более усовершенствованный механизм. У этого механизма несколько названий: z-буфер, w-буфер, буфер глубины. Размер z-буфера по количеству элементов совпадает с размером фонового и основного буферов. В z-буфер заносится z-компонента самого ближнего к камере объекта. В данном примере, там где синий треугольник перекрывает зелёный, в буфер глубины будут занесены z-координаты синего. Мы ещё поговорим о z-буферах более подробно в отдельном уроке.

Ортографическая / параллельная проекция (orthographic / parallel projection)

Операция при которой происходит уменьшение размерности пространства (было трёхмерное пространство, стало двухмерным) называется проекцией. Прежде всего нас интересует перспективная проекция, но сналача мы познакомимся с параллельной (parallel или orthographic projection).

Для вычисления параллельной проекции достаточно отбросить лишнюю координату. Если у нас есть точка в пространстве [ 3 3 3 ], то при параллельной проекции на плоскость z=1, она спроецируется в точку .

Перспективная проекция (perspective projection) на проекционную плоскость

В данном виде проекции все линии сходятся в одной точке. Именно так устроено наше зрение. И именно с помощью перспективной проекции моделируется "взгляд" во всех играх.

Сравните этот рисунок с рисунком показывающим однородные координаты из предыдущего урока. Чтобы из трёхмерного пространства перейти в двухмерное, нужно первые две компоненты векторов разделить на третью: [ x/z y/z z/z ] = [ x/z y/z 1 ].

Как я уже писал выше, проекционная плоскость может располагаться где угодно между ближней и дальней. Мы будем всегда размещать проекционную плоскость в z=1, но в этом уроке мы рассмотрим и другие варианты. Посмотрим на картинку:

Расстояние до проекционной плоскости от начала координат обозначим как d. Мы рассмотрим два случая: d=1 и d=5. Важный момент: третья компонента всех векторов после проекции должна быть равна d - все точки расположены в одной плоскости z=d. Этого можно добиться умножив все компоненты вектора на d: [ xd/z yd/z zd/z ]. При d=1, мы получим: [ x/z y/z 1 ], именно эта формула использовалась для преобразования однородных координат.

Теперь, если мы отодвинем проекционную плоскость в точку z=5 (соотвтественно d=5), мы получим: [ xd/z yd/z zd/z ] = [ 5x/z 5y/z 5 ]. Последняя формула проецирует все векторы пространства в одну плоскость, где d=5.
У нас здесь небольшая проблемка. Предыдущая формула работает с трёхмерными векторами. Но мы договорились использовать четырёхмерные векторы. Четвёртую компоненту в данном случае можно просто отбросить. Но мы не будем этого делать, так как её использование даёт некоторые специфические возможности, которые мы ещё обсудим.

Нужно найти общий делитель третьей и четвёртой компонент, при делении на который в третьей компоненте остаётся значение d, а в четвёртой единица. Делитель этот - d/z. Теперь из обычного вектора [ x y z 1 ] нам нужно получить вектор готовый к проекции (делению) [ x y z z/d ]. Делается это с помощью матрицы преобразования (проверьте результат умножив любой вектор на данную матрицу):

Последнее преобразование - это ещё не проекция. Здесь мы просто приводим все векторы к нужной нам форме. Напоминаю, что мы будем размещать проекционную плоскость в d=1, а значит векторы будут выглядеть вот так: [ x y z z ].

Матрица перспективного преобразования

Мы рассмотрим матрицу перспективного преобразования использующуюся в DirectX:

Теперь мы знаем для чего предназначен элемент _34. Мы также знаем, что элементы _11 и _22 масштабируют изображение по горизонтали и вертикали. Давайте посмотрим, что конкретно скрывается за именами xScale и yScale.

Данные переменные зависят от зон обзора, о которых мы говорили выше. Увеличивая или уменьшая эти углы, можно масштавбировать (scale или zoom) изображение - менять размер и соотношение сторон проекционной плоскости. Механизм масштабирования отдалённо напомниает масштабирование в фотоаппаратах/камерах - принцип очень похожий. Рассмотрим рисунок:

Разделим угол fov на две части и рассмотрим только одну половинку. Что мы тут видим: увеличивая угол fov/2 (а соответсвенно и угол fov), мы увеличиваем sin угла и уменьшаем cos. Это приводит к увеличению проекционной плоскости и соответственно к уменьшеню спроецированных объектов. Идеальным для нас углом будет fov/2 = P/4. Напоминаю, что угол в P/4 радиан равен 45 градусам. При этом fov будет равен 90 градусам. Чем для нас хорош угол в 45 градусов? В данном случае не происходит масштабирования, а cos(P/4)/sin(P/4)=1.

Теперь мы можем легко масштабировать картинку по вертикали (горизонтали), используя синус и косинус половины зоны обзора (функция котангенса в C++ называется cot):

yScale = cos(fovY/2)/sin(fovY/2) = cot(fovY/2)
В DirectX используется только вертикальная зона обзора (fovY), а масштабирование по горизонатли зависит от вертикальной зоны обзора и соотношения сторон.

Напоминаю, что окно в наших программах размером в 500x500. Соотношение сторон: 1 к 1. Поэтому переменные будут равны: xScale=1, yScale=1.

Соотношение сторон стандартного монитора/телевизора: 4:3. Этому соотношению соответствуют разрешения экрана: 640x480, 800x600, 1600x1200. Мы пока не будем касаться полноэкранного режима, но можем изменить размер окна программы. Вы можете поменять размер окна (в present parameters), например, на 640X480. Но чтобы все предметы не растянулись (квадраты будут выглядеть как прямоугольники), не забудьте поменять соответствующие переменные в проекционной матрице.

Чуть не забыл, форумула для xScale в DirectX:

xScale = yScale / соотношение сторон
Соотношения сторон задаются просто: 1/1, 4/3, 16/9 - это из стандартных.

Осталось выяснить назначение элементов _33, _34 матрицы перспективного преобразования. zf - z-координата дальней плоскости (от far - далеко), а zn - z-координата ближней (от near - близко). Обратите внимание, что элемент _43 = _33 * -zn.

Легче всего понять, что именно делают эти формулы, можно на примерах. Умножим стандартный вектор [ x y z w ] на матрицу представленную выше. Рекомендую вам сделать это, взяв лист бумаги и карандаш (надеюсь вы помните как перемножать две матрицы). Компоненты вектора примут следующий вид.

1-ая = x*xScale
2-ая = y*yScale
3-я = z*(zf/(zf-zn)) + w*(-(zn*zf)/(zf-zn)) = (zf/(zf-zn))*(z - w*zn)
4-ая = (w*z)/d
Совершим проекционное преобразование (разделим все элементы на 4-ую компоненту, при этом допустим, что d=1 и w=1):

1-ая = (d*x*xScale)/(w*z) = (x*xScale)/z
2-ая = (d*y*yScale)/(w*z) = (y*xScale)/z
3-я = (zf/(zf-zn))*(z - w*zn)*(w*d/z) = (zf/(zf-zn))*(1 - zn/z)
4-ая = 1
В результате мы получили вектор вида:

[ x/(z*xScale) y/(z*yScale) (zf/(zf-zn))*(1-zn/z) 1 ]
Теперь, если вы зададите конкретные значения zf и zn, то обнаружите следующее (для положительных значений): если вектор расположен до ближней плоскости, то z-компонента после преобразования будет меньше нуля, если вектор расположен за дальней плоскостью, то z-компонента будет больше единицы.

Нет никакой разници где именно расположены ближняя и дальняя плоскости: zn=1, zf=10 или zn=10, а zf=100 (или любые другие значения) - после преобразования видимая область будет располагаться в отрезке от нуля до единицы, включительно.

Именно для этого и предназначены формулы в элементах _33, _34 проекционной матрицы - спроецировать расстояние от ближней до дальней плоскости в отрезок . Проверьте это, вычислив значения нескольких векторов для конкретных значений zn,zf (да-да, на листке бумаги!!!).

Движок не перемещает корабль. Корабль остается на месте, а движок перемещает вселенную относительно его.

Это очень важная часть уроков, убедитесь что прочитали ее несколько раз и хорошо поняли.

Однородные координаты

До текущего момента мы оперировали 3х-мерными вершинами как (x, y, z) триплетами. Введем еще один параметр w и будем оперировать векторами вида (x, y, z, w).

Запомните навсегда, что:

• Если w == 1, то вектор (x, y, z, 1) - это позиция в пространстве.
• Если же w == 0, то вектор (x, y, z, 0) - это направление.

Что это дает нам? Ок, для поворота это ничего не меняет, так как и в случае поворота точки и в случае поворота вектора направления вы получаете один и тот же результат. Однако в случае переноса есть разница. Перенос вектора направления даст тот же самый вектор. Подробнее об этом остановимся позднее.

Однородные координаты позволяют нам с помощью одной математической формулы оперировать векторами в обоих случаях.

Матрицы трансформаций

Введение в матрицы

Проще всего представить матрицу, как массив чисел, со строго определенным количеством строк и столбцов. К примеру, матрица 2x3 выглядит так:

Однако в трехмерной графике мы будем использовать только матрицы 4x4, которые позволят нам трансформировать наши вершины (x, y, z, w). Трансформированная вершина является результатом умножения матрицы на саму вершину:

Матрица x Вершина (именно в этом порядке!!) = Трансформир. вершина

Довольно просто. Мы будем использовать это довольно часто, так что имеет смысл поручить это компьютеру:

В C++, используя GLM:

glm :: mat4 myMatrix ; glm :: vec4 myVector ; glm :: // Обратите внимание на порядок! Он важен!

В GLSL:

mat4 myMatrix ; vec4 myVector ; // Не забудьте тут заполнить матрицу и вектор необходимыми значениями vec4 transformedVector = myMatrix * myVector ; // Да, это очень похоже на GLM:)

Попробуйте поэкспериментировать с этими фрагментами.

Матрица переноса

Матрица переноса выглядит так:

где X, Y, Z - это значения, которые мы хотим добавить к нашему вектору.

Значит, если мы захотим перенести вектор (10, 10, 10, 1) на 10 юнитов в направлении X, то мы получим:

… получим (20, 10, 10, 1) однородный вектор! Не забывайте, что 1 в параметре w, означает позицию, а не направление и наша трансформация не изменила того, что мы работаем с позицией.

Теперь посмотрим, что случится, если вектор (0, 0, -1, 0) представляет собой направление:

… и получаем наш оригинальный вектор (0, 0, -1, 0). Как было сказано раньше, вектор с параметром w = 0 нельзя перенести.

И самое время перенести это в код.

В C++, с GLM:

#include // после glm :: mat4 myMatrix = glm :: translate (glm :: mat4 (), glm :: vec3 (10.0 f , 0.0 f , 0.0 f )); glm :: vec4 myVector (10.0 f , 10.0 f , 10.0 f , 0.0 f ); glm :: vec4 transformedVector = myMatrix * myVector ;

В GLSL:

vec4 transformedVector = myMatrix * myVector ;

По факту, вы никогда не будете делать это в шейдере, чаще всего вы будете выполнять glm::translate() в C++, чтобы вычислить матрицу, передать ее в GLSL, а уже в шейдере выполнить умножение

Единичная матрица

Это специальная матрица, которая не делает ничего, но мы затрагиваем ее, так как важно помнить, что A умноженное на 1.0 дает A:

В C++ :

glm :: mat4 myIdentityMatrix = glm :: mat4 (1.0 f );

Матрица масштабирования

Выглядит также просто:

Значит, если вы хотите применить масштабирование вектора (позицию или направление - это не важно) на 2.0 во всех направлениях, то вам необходимо:

Обратите внимание, что w не меняется, а также обратите внимание на то, что единичная матрица - это частный случай матрицы масштабирования с коэффициентом масштаба равным 1 по всем осям. Также единичная матрица - это частный случай матрицы переноса, где (X, Y, Z) = (0, 0, 0) соответственно.

В C++ :

// добавьте #include и #include glm :: mat4 myScalingMatrix = glm :: scale (2.0 f , 2.0 f , 2.0 f );

Матрица поворота

Сложнее чем рассмотренные ранее. Мы опустим здесь детали, так как вам не обязательно знать это точно для ежедневного использования. Для получения более подробной информации можете перейти по ссылке Matrices and Quaternions FAQ (довольно популярный ресурс и возможно там доступен ваш язык)

В C++ :

// добавьте #include и #include glm :: vec3 myRotationAxis ( ?? , ?? , ?? ); glm :: rotate ( angle_in_degrees , myRotationAxis );

Собираем трансформации вместе

Итак, теперь мы умеем поворачивать, переносить и масштабировать наши векторы. Следующий шагом было бы неплохо объединить трансформации, что реализуется по следующей формуле:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector ;

ВНИМАНИЕ! Эта формула на самом деле показывает, что сначала выполняется масштабирование, потом поворот и только в самую последнюю очередь выполняется перенос. Именно так работает перемножение матриц.

Обязательно запомните в каком порядке все это выполняется, потому что порядок действительно важен, в конце концов вы можете сами это проверить:

• Сделайте шаг вперед и повернитесь влево
• Повернитесь влево и сделайте шаг вперед

Разницу действительно важно понимать, так как вы постоянно будете с этим сталкиваться. К примеру, когда вы будете работать с игровыми персонажами или какими-то объектами, то всегда сначала выполняйте масштабирование, потом поворот и только потом перенос.

На самом деле, приведенный выше порядок - это то, что вам обычно нужно для игровых персонажей и других предметов: сначала масштабируйте его, если это необходимо; затем установливаете его направление, а затем перемещаете его. Например, для модели судна (повороты удалены для упрощения):

• Неправильный путь:
  • Вы переносите корабль на (10, 0, 0). Его центр теперь находится в 10 единицах от начала координат.
  • Вы масштабируете свой корабль в 2 раза. Каждая координата умножается на 2 “относительно исходной”, что далеко… Итак, вы попадаете в большой корабль, но его центр 2 * 10 = 20. Не то, что вы хотели.
• Правильный путь:
  • Вы масштабируете свой корабль в 2 раза. Вы получаете большой корабль, с центром в начале координат.
  • Вы переносите свой корабль. Он по прежнему того же размера и на правильном расстоянии.

В C++, с GLM:

glm :: mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix ; glm :: vec4 myTransformedVector = myModelMatrix * myOriginalVector ;

В GLSL:

mat4 transform = mat2 * mat1 ; vec4 out_vec = transform * in_vec ;

Мировая, видовая и проекционная матрицы

До конца этого урока мы будем полагать, что знаем как отображать любимую 3D модель из Blender - обезьянку Suzanne.

Мировая, видовая и проекционная матрицы - это удобный инструмент для разделения трансформаций.

Мировая матрица

Эта модель, также, как и наш красный треугольник задается множеством вершин, координаты которых заданы относительно центра объекта, т. е. вершина с координатами (0, 0, 0) будет находиться в центре объекта.

Далее мы бы хотели перемещать нашу модель, так как игрок управляет ей с помощью клавиатуры и мышки. Все, что мы делаем - это применяем масштабирование, потом поворот и перенос. Эти действия выполняются для каждой вершины, в каждом кадре (выполняются в GLSL, а не в C++!) и тем самым наша модель перемещается на экране.

Теперь наши вершины в мировом пространстве. Это показывает черная стрелка на рисунке. Мы перешли из пространства объекта (все вершины заданы относительно центра объекта) к мировому пространству (все вершины заданы относительно центра мира).

Схематично это показывается так:

Видовая матрица

Еще раз процитируем Футураму:

Движок не перемещает корабль. Корабль остается на том же месте, а движок перемещает вселенную вокруг него.

Попробуйте представить это применительно к камере. Например, если вы хотите сфотографировать гору, то вы не перемещаете камеру, а перемещаете гору. Это не возможно в реальной жизни, но это невероятно просто в компьютерной графике.

Итак, изначально ваша камера находится в центре мировой системы координат. Чтобы переместить мир вам необходимо ввести еще одну матрицу. Допустим, что вы хотите переместить камеру на 3 юнита ВПРАВО (+X), что будет эквивалентом перемещения всего мира на 3 юнита ВЛЕВО (-X). В коде это выглядит так:

// Добавьте #include и #include glm :: mat4 ViewMatrix = glm :: translate (glm :: mat4 (), glm :: vec3 (- 3.0 f , 0.0 f , 0.0 f ));

Опять же, изображение ниже полностью показывает это. Мы перешли из мировой системы координат (все вершины заданы относительно центра мировой системы) к системе координат камеры (все вершины заданы относительно камеры):

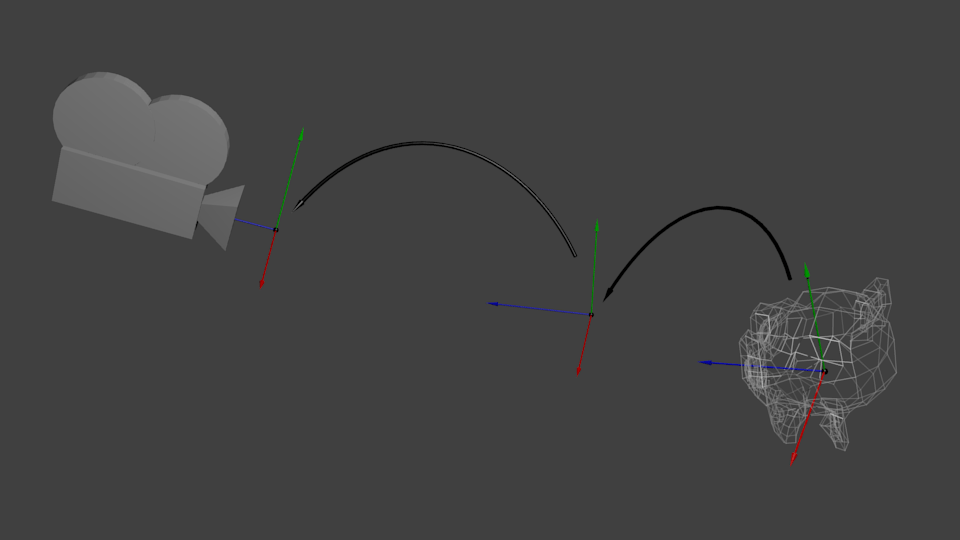
И пока ваш мозг переваривает это, мы посмотрим на функцию, которую предоставляет нам GLM, а точнее на glm::LookAt:

glm :: mat4 CameraMatrix = glm :: LookAt ( cameraPosition , // Позиция камеры в мировом пространстве cameraTarget , // Указывает куда вы смотрите в мировом пространстве upVector // Вектор, указывающий направление вверх. Обычно (0, 1, 0) );

А вот диаграмма, которая показывает то, что мы делаем:

Однако это еще не конец.

Проекционная матрица

Итак, теперь мы находимся в пространстве камеры. Это означает, что вершина, которая получит координаты x == 0 и y == 0 будет отображаться по центру экрана. Однако, при отображении объекта огромную роль играет также дистанция до камеры (z). Для двух вершин, с одинаковыми x и y, вершина имеющая большее значение по z будет отображаться ближе, чем другая.

Это называется перспективной проекцией:

И к счастью для нас, матрица 4х4 может выполнить эту проекцию :

// Создает действительно трудночитаемую матрицу, но, тем не менее это стандартная матрица 4x4 glm :: mat4 projectionMatrix = glm :: perspective ( glm :: radians (FoV ), // Вертикальное поле зрения в радианах. Обычно между 90° (очень широкое) и 30° (узкое) 4.0 f / 3.0 f , // Отношение сторон. Зависит от размеров вашего окна. Заметьте, что 4/3 == 800/600 == 1280/960 0.1 f , // Ближняя плоскость отсечения. Должна быть больше 0. 100.0 f // Дальняя плоскость отсечения. );

Мы перешли из Пространства Камеры (все вершины заданы относительно камеры) в Однородное пространство (все вершины находятся в небольшом кубе. Все, что находится внутри куба - выводится на экран).

Теперь посмотрим на следующие изображения, чтобы вы могли лучше понять что же происходит с проекцией. До проецирования мы имеем синие объекты в пространстве камеры, в то время как красная фигура показывает обзор камеры, т. е. все то, что видит камера.

Применение Проекционной матрицы дает следующий эффект:

На этом изображении обзор камеры представляет собой куб и все объекты деформируются. Объекты, которые находятся ближе к камере отображаются большими, а те, которые дальше - маленькими. Прямо как в реальности!

Вот так это будет выглядеть:

Изображение является квадратным, поэтому следующие математические трансформации применяются, чтобы растянуть изображение согласно актуальным размерам окна:

И это изображение является тем, что на самом деле будет выведено.

Объединяем трансформации: матрица ModelViewProjection

… Просто стандартные матричные преобразования, которые вы уже полюбили!

// C++ : вычисление матрицы glm :: mat4 MVPmatrix = projection * view * model ; // Запомните! В обратном порядке!

// GLSL: применение матрицы transformed_vertex = MVP * in_vertex ;

Совмещаем все вместе

• Первый шаг - создание нашей MVP матрицы. Это должно быть сделано для каждой модели, которую вы отображаете.

// Проекционная матрица: 45° поле обзора, 4:3 соотношение сторон, диапазон: 0.1 юнит <-> 100 юнитов glm :: mat4 Projection = glm :: perspective (glm :: radians (45.0 f ), 4.0 f / 3.0 f , 0.1 f , 100.0 f ); // Или, для ортокамеры glm :: mat4 View = glm :: lookAt ( glm :: vec3 (4 , 3 , 3 ), // Камера находится в мировых координатах (4,3,3) glm :: vec3 (0 , 0 , 0 ), // И направлена в начало координат glm :: vec3 (0 , 1 , 0 ) // "Голова" находится сверху ); // Матрица модели: единичная матрица (Модель находится в начале координат) glm :: mat4 Model = glm :: mat4 (1.0 f ); // Индивидуально для каждой модели // Итоговая матрица ModelViewProjection, которая является результатом перемножения наших трех матриц glm :: mat4 MVP = Projection * View * Model ; // Помните, что умножение матрицы производиться в обратном порядке

• Второй шаг - передать это в GLSL:

// Получить хэндл переменной в шейдере // Только один раз во время инициализации. GLuint MatrixID = glGetUniformLocation (programID , "MVP" ); // Передать наши трансформации в текущий шейдер // Это делается в основном цикле, поскольку каждая модель будет иметь другую MVP-матрицу (как минимум часть M) glUniformMatrix4fv (MatrixID , 1 , GL_FALSE , & MVP [ 0 ][ 0 ]);

• Третий шаг - используем полученные данные в GLSL, чтобы трансформировать наши вершины.

// Входные данные вершин, разные для всех исполнений этого шейдера. layout (location = 0 ) in vec3 vertexPosition_modelspace ; // Значения, которые остаются постоянными для всей сетки. uniform mat4 MVP ; void main (){ // Выходная позиция нашей вершины: MVP * position gl_Position = MVP * vec4 (vertexPosition_modelspace , 1 ); }

• Готово! Теперь у нас есть такой же треугольник как и в Уроке 2, все так же находящийся в начале координат (0, 0, 0), но теперь мы его видим в перспективе из точки (4, 3, 3).

В Уроке 6 вы научитесь изменять эти значения динамически, используя клавиатуру и мышь, чтобы создать камеру, которую вы привыкли видеть в играх. Но для начала мы узнаем как придать нашем моделям цвета (Урок 4) и текстуры (Урок 5).

Задания

• Попробуйте поменять значения glm::perspective
• Вместо использования перспективной проекции попробуйте использовать ортогональную (glm:ortho)
• Измените ModelMatrix для перемещения, поворота и масштабирования треугольника
• Используйте предыдущее задание, но с разным порядком операций. Обратите внимание на результат.