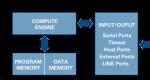
يتم تطبيق طريقة النمذجة الرياضية على ثلاث مراحل.
المرحلة الأولى.تحديد الهدف من النمذجة. يجب أن يستبدل النموذج الكائن الحقيقي بدرجة من التجريد تكون أكثر فائدة لتحقيق هدف معين.
المرحلة الثانية.خلق النموذج المفاهيمي، أي وصف ذو معنى للكائن النموذجي. يتضمن النموذج المفاهيمي المعلومات التالية:
- تكوين وهيكل الكائن؛
- علاقات السبب والنتيجة بين معلمات الكائن؛
- عدد المعلمات الكافي لوصف الكائن بشكل مناسب؛
- فئة الكائن قيد الدراسة والنموذج الذي يتم إنشاؤه؛
- ظروف تشغيل الكائن.
في هذه المرحلة، يتعين على مطور النموذج الرياضي حل ثلاث مسائل.
المشكلة 1.إيجاد حل وسط بين بساطة النموذج وملاءمته للكائن الحقيقي.
أي كائن حقيقي في عملية الأداء يتأثر بعدة عوامل (خارجية وداخلية). كلما زاد عدد العوامل التي يتم أخذها في الاعتبار في النموذج، أصبح النموذج أكثر ملاءمة. ومع ذلك، يمكن أن يصبح الأمر معقدًا ومرهقًا لدرجة ظهور المشكلات التالية:
- عدم وجود طرق فعالة لدراسة مثل هذا النموذج؛
- الزيادة في تكاليف النمذجة سوف تتجاوز الزيادة في التأثير من إدخال النموذج.
لا يمكنك الذهاب إلى الطرف الآخر - المبالغة في تبسيط النموذج من خلال إهمال تأثير العوامل المهمة. سيؤدي ذلك إلى عدم كفاية النموذج، وبالتالي تشويه نتائج المحاكاة. لذلك، من الضروري الاختيار الصارم للعوامل المؤثرة، وتمايزها الواضح في الأساسية (س)و قاصر (ب).يجب أن تؤخذ العوامل الرئيسية في الاعتبار في النموذج، ويجب التخلص من العوامل الثانوية (الشكل 1.9). هذا لا يسبب ضررا كبيرا لجودة النموذج.
المشكلة 2.تعريف حدود قابلية التطبيقالنموذج الذي تم إنشاؤه.
تعتبر النتائج التي تم الحصول عليها باستخدام نموذج معين صالحة فقط ضمن الشروط المحددة (ضمن مجال الملاءمة).
مثال 1.13. أنشئ نموذجًا رياضيًا يصف عملية سقوط الجسم على الأرض.
وتستند هذه الظاهرة إلى قانون الجذب العام الذي صاغه نيوتن: أي جسمين يتجاذبان بقوة تتناسب طرديا مع حاصل ضرب كتلتهما، وعكسيا مع مربع المسافة بينهما.
إذا اعتبرنا الكرة المعدنية والأرض هذين الجسمين، فإنه في لغة الرياضيات يمكن وصف سقوط الكرة بالعلاقة:
 ,
(1.6)
,
(1.6)
أين  - ثابت؛
- ثابت؛
m و МЗ - كتلة الكرة والأرض،
R هي المسافة بين مراكز جذب الأجسام.
وفقًا لقانون نيوتن الثاني، إذا أثرت قوة F على جسم، فإن حركته توصف بالعلاقة:
 (1.7)
(1.7)
وبما أن عملية سقوط الجسم تعتبر، فيجب استبدالها بتسارع السقوط الحر  . عندها سيأخذ نموذج سقوط الكرة الشكل التالي:
. عندها سيأخذ نموذج سقوط الكرة الشكل التالي:
 أو
أو  – (1.8)
– (1.8)
هذا هو النموذج العام. الآن من الضروري تحديده للظروف التجريبية المحددة. يتم إجراء تجربة الكرة في المختبر (أي بالقرب من سطح الأرض). ولذلك يمكننا أن نفترض أن المسافة بين مركزي الأرض والكرة تساوي نصف قطر الأرض: R = R Z. فيأخذ النموذج الرياضي الصورة:
 (1.9)
(1.9)
يتيح لنا هذا النموذج تقديم وصف شامل لعملية سقوط الكرة في أي لحظة زمنية t: لتحديد الارتفاع h الذي تقع عنده الكرة، وكذلك سرعتها v:
 (1.10)
(1.10)
 (1.11)
(1.11)
حدود قابلية التطبيقهذا النموذج:
- سقوط الجسم من ارتفاع صغير لا يكاد يذكر مقارنة بنصف قطر الأرض؛
- الجسم ذو شكل مدمج وكتلة كافية؛
- يمكن إهمال عامل مقاومة الهواء.
إذا تم انتهاك واحد على الأقل من هذه الشروط، فلن يكون هذا النموذج كافيا. على سبيل المثال، لا يمكن استخدام هذا النموذج لوصف العمليات التالية: هبوط المظلي، سقوط أوراق الشجر من شجرة، سقوط شظية نيزك على الأرض، وما إلى ذلك.
في كل حالة من الحالات المذكورة، يتم ملاحظة تأثير عوامل لم يتم حسابها مسبقًا مثل قوة مقاومة الهواء، وجاذبية القمر، والشمس، وانخفاض كثافة الغلاف الجوي مع الارتفاع، ودوران الأرض، والرياح التي تهب بشكل مختلف بدرجات مختلفة. الارتفاعات، هو الاختلاف الفعلي في شكل الأرض عن الكرة (وهو جسم ذو شكل هندسي أكثر تعقيدًا).
المشكلة 3.تعريف مستوى التفاصيلالكائن قيد الدراسة.
أي نظام مادي هو عبارة عن مجموعة من العناصر. ويمكن تقسيم كل عنصر بدوره إلى عناصر فرعية. من الناحية النظرية، يمكن أن تكون عملية التقطيع لا نهاية لها. مهمة الباحث هي اختيار المستوى الأمثل من التفاصيل للكائن النموذجي. يتم تحديد مستوى التفاصيل من خلال الغرض من النمذجة ودرجة المعرفة بخصائص عناصر الكائن.
يُنصح بإجراء التفاصيل إلى هذا المستوى الذي يمكن عنده تحديد اعتماد معلمات إشارات الخرج على معلمات إشارات الإدخال لكل عنصر. تؤدي الرغبة في زيادة مستوى التفاصيل إلى إرهاق النموذج بشكل مفرط وزيادة حادة في أبعاده.
المرحلة الثالثة.تكوين نموذج رياضي، أي تسجيل النموذج في شكل رسمي:
– جميع العلاقات مكتوبة في شكل تحليلي.
- يتم التعبير عن الشروط المنطقية في شكل أنظمة عدم المساواة؛
- العمليات العشوائية تستبدلها بالنماذج القياسية.
المرحلة الرابعة.دراسة النموذج الرياضي. أدوات البحث هي الأساليب العددية والتحليلية.
المرحلة الخامسة.تحليل نتائج النمذجة مع الاستنتاج اللاحق حول مدى كفاية النموذج، أو الحاجة إلى تعديله، أو عدم ملاءمته.
- 1. تمت ترجمة المشكلة إلى لغة الرياضيات.
- 2. يتم حلها باستخدام الطرق الرياضية.
- 3. يتم تفسير النتائج التي تم الحصول عليها وترجمتها مرة أخرى إلى اللغة الطبيعية.
عند تطوير نموذج رياضي للبنية التقنية، نقوم في البداية بإنشاء نموذج يعتمد على مفاهيم العلوم الطبيعية. في الواقع، من أجل وصف رحلة صاروخ فضائي رياضيًا، من الضروري استخدام معلومات من الفيزياء والكيمياء والعلوم ذات الصلة، لتطبيق بيانات المشكلة الأساسية، المعروفة على نطاق واسع في هذه العلوم، بناءً على الفرضيات والتجريدات المناسبة. ويمكن اعتبار العلوم الطبيعية نفسها، التي تستخدم الأوصاف الرياضية، نماذج رياضية.
إن مشكلة ربط خصائص الأشياء بخصائصها العددية والهندسية هي مشكلة إمكانية قياس خصائصها. في كل مستوى هيكلي لتنظيم المادة، هناك قوانين موضوعية تحدد العلاقة بين الأشياء والظواهر في العالم الحقيقي. على المستوى المادي، باعتباره أبسط نسبيًا، من الممكن أن تعكس بشكل كامل من خلال العلاقات الكمية الخصائص النوعية العميقة للعملية قيد الدراسة. في العلوم الكيميائية والبيولوجية والاجتماعية التي تدرس أشكالًا أكثر تعقيدًا من تنظيم وحركة المادة، تصبح مسألة ما إذا كانت خصائص الأشياء قيد الدراسة تتوافق مع الخصائص العددية التي تسمح بقياسها أكثر صعوبة، وبالتالي، يتم تضييق إمكانيات النمذجة الرياضية. باستخدام حتى أجهزة الكمبيوتر الأكثر تقدمًا، من المستحيل تحقيق الرياضيات المطلقة لمعرفتنا: فالتقديرات الكمية لا يمكنها استنفاد الخصائص النوعية لشيء ما. فكرة خلق الذكاء الاصطناعي باستخدام الوسائل التكنولوجية، والتي أسرت الكثير من الباحثين، بدت حقيقية تمامًا حتى وقت قريب. والآن يحتاج مصطلح "الذكاء الاصطناعي" إلى علامتي تنصيص: فالنموذج الرياضي للدماغ، مهما بلغ من الكمال، لن يتمكن من عكس الجانب النوعي للنشاط الإبداعي البشري، حتى لو تم البحث عن كل الخيارات الممكنة للنشاط الإبداعي البشري. وتحدث "حركة" الفكر بسرعة مذهلة لأجهزة الكمبيوتر الحديثة. ولكن في حل المشكلات الفنية، والتي تعتمد في أغلب الأحيان على القوانين الفيزيائية للعالم المحيط، فإن النمذجة الرياضية هي طريقة بحث فعالة.
تم فصل العلوم التقنية عن العلوم الرياضية والطبيعية نتيجة لتجسيد وتطبيق المعرفة الأساسية في المجالات الفردية للنشاط الهندسي. حدث هذا فقط في نهاية القرن التاسع عشر. يتم تحديد تطور أي علم تقني إلى حد كبير من خلال مكونه الأساسي. تبدأ النمذجة الرياضية بإنشاء اتصالات يخضع لها وجود الكائن. في هذه الحالة، تعتمد النمذجة على معرفة تخصصات فنية محددة، مثل “تصميم الغلايات”، “الركائز والأساسات”، “محركات الاحتراق الداخلي”، إلخ. (حسب موضوع الدراسة). علاوة على ذلك، يتم تعميم هذه المعرفة على مستوى المفاهيم الأساسية المقابلة للعلوم التقنية العامة، على سبيل المثال، "قوة المواد"، "نظرية الآليات والآلات"، "الأسس النظرية للهندسة الكهربائية". عند حل المهام الهندسية، يتم تقليل هذه المعرفة إلى حد كبير إلى الفيزياء أو الكيمياء. لذلك، فإن الخطوة الوسيطة في إنشاء نموذج رياضي هي رسم تخطيطي يعكس فكرة كائن على مستوى العلوم الطبيعية، موصوفًا بالقوانين الأساسية للعالم المادي التي تميز عمل هذا الهيكل. ويكمل الوصف الرياضي لهذه القوانين المرحلة الأولى من النمذجة الرياضية. يجب أن ترتبط المراحل اللاحقة لإنشاء النموذج الرياضي بالتحقق من الفرضيات المقبولة وتوضيحها. يحدث الوصف العلمي الطبيعي على مستوى تجريد العلوم الطبيعية، ثم "تواصل" الرياضيات التجريد، وتنتقل إلى مستواها الأعلى نوعيًا، مع الأخذ في الاعتبار الصور المثالية الخاصة بالرياضيات.
يمكن اختزال نفس المشكلة التقنية في نماذج رياضية مختلفة، بينما في نفس الوقت النماذج الرياضية نفسها، التي أصبحت بالفعل كلاسيكية، قابلة للتطبيق على حل مجموعة واسعة من المشاكل. ولذلك، فإن المراسلات بين المشاكل التي تنشأ في الممارسة العملية والنماذج الرياضية متعددة القيم. كما يعتقد العالم والمعلم ف. Uspensky، من المنطقي، قياسا على الصور الفنية، التحدث عن الصور الرياضية كشكل محدد من انعكاس الواقع. الواقع معقد للغاية (وفي التكنولوجيا الحديثة يعد هذا التعقيد استثنائيًا) لدرجة أن عملية التبسيط في الظروف الواقعية تصبح وسيلة ضرورية للغاية ومبررة لدراسة شيء ما. يتمثل فن اختيار النموذج الرياضي في تحقيق وحدة متناغمة من البساطة والوضوح في فهم موضوع البحث، والذي يتوافق أيضًا مع مهام الإبداع الفني. في بعض الأحيان، بالنسبة للأشياء التي لم تتم دراسة خصائصها إلا قليلا، يتم إنشاء ما يسمى بالنموذج الافتراضي، والذي لا يمكن تأكيده في كل شيء من خلال الممارسة - على سبيل المثال، نموذج للعالم الصغير. وفي الوقت نفسه، يسمح لنا نموذج الفرضية هذا بتوسيع فهمنا للعالم من حولنا. لحل العديد من المهام الهندسية، تم تطوير نماذج رياضية عالمية للغاية، والتي تعتبر بالفعل كلاسيكية. لقد تم اختبار الاستنتاجات النظرية التي تم الحصول عليها بمساعدتهم بشكل متكرر في الممارسة العملية، وتم تحديد حدود إمكانية تطبيق هذه النماذج. تتيح مثل هذه النماذج الرياضية استخدام الخبرة المكتسبة في حل المشكلات المعروفة بالفعل لدراسة المشكلات الجديدة.
يختلف علماء الرياضيات عن بعضهم البعض في أنهم يتحدثون مع بعضهم البعض ويكتبون "بلغة رياضية" خاصة. باستخدام اللغة الرياضية، يمكنك إنشاء نماذج رياضية لمواقف حقيقية. في عملية حل المشكلة، يتم تمييز ثلاث مراحل من النمذجة الرياضية: 1) وضع نموذج رياضي، 2) العمل مع نموذج رياضي، 3) الإجابة على سؤال المشكلة. دعونا نلقي نظرة على بعض الأمثلة التي تناقش مراحل النمذجة الرياضية.
سار السائح لمدة ساعتين من النقطة أ إلى النقطة ب، ثم عند النقطة ب استقل قاربًا تبلغ سرعته 4 أضعاف سرعة السائح كمشاة، وركب القارب لمدة ساعة ونصف إلى النقطة ج. استقل حافلة تبلغ سرعتها ضعف سرعة القارب، وركب عليها لمدة ساعتين حتى النقطة د. ما هي السرعة التي سافر بها السائح في الحافلة إذا علم أن طريقه بالكامل من أ إلى D كان 120 كم؟
حل.
اجعل x km/h هي سرعة المشاة. في ساعتين سوف يقطع مسافة 2 كم.
ويستنتج من الشرط أن سرعة القارب 4 كم/ساعة. في 1.5 ساعة سيقطع القارب مسافة 4 × 1.5 كم، أي. 6 كم.
من الشرط يستنتج أن سرعة الحافلة هي 2x4x كم/ساعة، 8x كم/ساعة. خلال ساعتين ستسافر الحافلة مسافة 8xH2 كم، أي. 16 كم.
كامل المسار من A إلى D يساوي: 2x+6x+16x وهو حسب الشرط 120 كم. وبالتالي، 2س+6س+16س=120.
وهذا نموذج رياضي للمشكلة.
المرحلة الثانية. العمل مع النموذج المترجم.
بإضافة وحيدات الحد 2x، 6x، 16x، نحصل على 24x. وهذا يعني 24س=120، ومنها نجد س=5.
لقد أخذنا سرعة المشاة على أنها x، وهي تساوي 5 كم/ساعة. سرعة القارب أكبر 4 مرات، أي. 20 كم/ساعة، وسرعة الحافلة أعلى مرتين، أي. 40 كم/ساعة.
إجابة: سرعة الحافلة 40 كم/ساعة.
تقع النقاط A وB وC على الطريق السريع فوق بعضها البعض. المسافة بين A و B هي 16 كم. غادر أحد المشاة B باتجاه C. بعد ساعتين من ذلك، غادر راكب دراجة A في اتجاه C، وكانت سرعته أكبر بمقدار 6 كم/ساعة من سرعة أحد المشاة. بعد مرور ٤ ساعات من المغادرة، لحق راكب الدراجة بالمشاة عند النقطة C. ما المسافة من B إلى C؟
حل.
المرحلة الأولى. رسم نموذج رياضي .
افترض أن x km/h هي سرعة المشاة، ثم (x+6) km/h هي سرعة راكب الدراجة.
قطع راكب الدراجة المسافة من A إلى C في 4 ساعات، مما يعني أن هذه المسافة يتم التعبير عنها بالصيغة 4(x+6) km؛ بمعنى آخر، AC=4(x+6).
مشى المشاة المسافة من B إلى C في 6 ساعات (بعد كل شيء، قبل مغادرة الدراج، كان بالفعل على الطريق لمدة ساعتين)، لذلك، يتم التعبير عن هذه المسافة بالصيغة 6x كم، وبعبارة أخرى، BC = 6x.
وبالشرط، نعلم أن النقاط A وB وC تتبع بعضها البعض، وبالتالي AC-BC = AB، أي. ايه سي-بي سي = 16. هذا هو الأساس لوضع نموذج رياضي للمشكلة. تذكر أن AC=4(x+6)، BC=6x؛ لذلك،
لحل المعادلة، عليك أولًا ضرب أحادية الحد 4 في ذات الحدين x + 6، نحصل على 4x + 24. ثانيًا، سيتعين عليك طرح أحادية الحد 6x من ذات الحدين 4x+24:
4س+24-6س=24-2س.
وبعد هذه التحولات تأخذ المعادلة شكلاً أبسط:
المرحلة الثالثة. الإجابة على سؤال المشكلة.
لقد حصلنا على x=4، مما يعني أن سرعة المشاة هي 4 كم/ساعة. لكن هذا ليس ما نحتاج إلى إيجاده؛ في المشكلة نحتاج إلى إيجاد المسافة من B إلى C. لقد أثبتنا أن BC = 6x، مما يعني أن BC = 6Х4 = 24.
إجابة: المسافة من B إلى C هي 24 كم.
طفو القارب في النهر لمدة 3 ساعات و12 دقيقة، ثم عكس التيار لمدة 1.5 ساعة، أوجد سرعة القارب إذا علم أن سرعة تيار النهر هي 2 كم/ساعة، والمسافة الإجمالية التي قطعها القارب. القارب 41 كم.
حل.
المرحلة الأولى. رسم نموذج رياضي .
افترض أن x km/h هي سرعة القارب، فإنه يطفو مع التيار بسرعة (x+2) km/h، وضد التيار بسرعة (x_2) km/h.
طاف القارب في النهر لمدة 3 ساعات و12 دقيقة. وبما أن السرعة يتم التعبير عنها بالكيلومتر/الساعة، فيجب تسجيل هذا الوقت بالساعات. لدينا: 12 دقيقة = 12/60 ساعة = 1/5 ساعة = 0.2 ساعة، وهذا يعني 3 ساعات و12 دقيقة = 3.2 ساعة، وبسرعة (x + 2) كم/ساعة 3، 2(س+2) كم.
طاف القارب عكس التيار لمدة 1.5 ساعة، وخلال هذه المدة، وبسرعة (x-2) كم/ساعة، قطع القارب مسافة 1.5 (x-2) كم.
وبحسب الشرط فإن مسارها بالكامل كان 41 كيلومترا. وبما أنه يتكون من مسار مع التيار ومسار ضد التيار، فإننا نحصل على:
3.2(س+2)+1.5(س-2)=41.
هذه المعادلة هي نموذج رياضي للمشكلة.
المرحلة الثانية. العمل مع النموذج الرياضي المترجم.
كما هو الحال دائمًا، في هذه المرحلة، نفكر فقط في كيفية حل النموذج - المعادلة، وليس في مصدر هذا النموذج. على الجانب الأيسر من المعادلة، دعونا نضرب أحادية الحد 3.2 في ذات الحدين x+2، ووحيدة الحد 1.5 في ذات الحدين x-2، ثم نضيف متعددات الحدود الناتجة:
3.2x+6.4+1.5x-3=41;
المرحلة الثالثة. الإجابة على سؤال المشكلة.
والسؤال هو: ما هي سرعة القارب، أي؟ ما هو x يساوي؟ لكن الإجابة على هذا السؤال قد تم تلقيها بالفعل: x=8.
إجابة:سرعة القارب هي 8 كم/ساعة.
في الصف السابع، لم تأت فتاة وخمسة أولاد إلى المدرسة يوم الاثنين. وفي الوقت نفسه، تبين أن عدد الفتيات في الفصل أكبر مرتين من عدد الأولاد. ولم يحضر صبي وتسع فتيات يوم الثلاثاء. علاوة على ذلك، تبين أن عدد الأولاد أكبر بمقدار 1.5 مرة من عدد الفتيات. يوم الأربعاء جاء جميع الطلاب إلى الفصل. كم عدد الطلاب الذين كانوا حاضرين في الفصل يوم الأربعاء في الصف السابع؟
حل.
المرحلة الأولى. رسم نموذج رياضي .
اجعل x هو عدد البنات و y عدد الأولاد في الصف السابع.
يوم الاثنين كان هناك (س-1) فتيات، (ص-5) أولاد. اتضح أن هناك ضعف عدد الفتيات، أي.
يوم الثلاثاء كان هناك (x-9) فتيات، (y-1) أولاد. اتضح أن عدد الأولاد أكبر بمقدار 1.5 مرة، أي.
يتم تجميع النموذج الرياضي للموقف:
المرحلة الثانية. العمل مع النموذج الرياضي المترجم.
أولا، دعونا نبسط كل معادلة في النظام.
بالنسبة للمعادلة الأولى لدينا:

وبالنسبة للمعادلة الثانية لدينا:
وبذلك حصلنا على النظام التالي من معادلتين خطيتين بمتغيرين:
نحن نحل النظام بطريقة الاستبدال. من المعادلة الأولى للنظام نجد: x=2y-9. وبتعويض هذه النتيجة بدلاً من x في المعادلة الثانية للنظام نجد: x = 2y-9. لنعوض بهذه النتيجة بدلاً من x في المعادلة الثانية للنظام. نحن نحصل:

بما أن x=2y-9، فإن x=2Х13-9=17.
لذا، x=17, y=13 هو الحل للنظام.
المرحلة الثالثة. الإجابة على سؤال المشكلة.
السؤال هو: كم عدد طلاب الصف السابع الذين كانوا في الفصل يوم الأربعاء عندما وصل جميع الطلاب. بما أن x=17، y=13، أي كان هناك 17 فتاة و 13 فتى في الفصل، نستنتج: في المجموع هناك 17 + 13 = 30 طالبًا في الفصل.
إجابة: 30 طالبا.
الطريقة الحسابية. حل المشكلة باستخدام الطريقة الحسابية يعني العثور على إجابة متطلبات المشكلة عن طريق إجراء العمليات الحسابية على الأرقام. يمكن حل نفس المشكلة في كثير من الحالات باستخدام طرق حسابية مختلفة. تعتبر المشكلة محلولة بطرق مختلفة إذا اختلفت حلولها في الروابط بين البيانات والبيانات المطلوبة التي تشكل أساس الحلول، أو في تسلسل استخدام هذه الاتصالات.
مثال. 82 طالبًا يغنون في الجوقة ويرقصون، و32 طالبًا يرقصون والجمباز الإيقاعي، و78 طالبًا يغنون في الجوقة ويمارسون الجمباز الإيقاعي. كم عدد الطلاب الذين يغنون في الجوقة ويمارسون الرقص والجمباز الإيقاعي بشكل منفصل إذا كان من المعروف أن كل طالب يفعل شيئًا واحدًا فقط؟
1) 82+32+78=192 شخص. - مضاعفة عدد الطلاب الذين يغنون في الجوقة والرقص والجمباز الإيقاعي؛
2) 192÷2 = 96 شخصًا. - الغناء في جوقة، والرقص والجمباز الإيقاعي؛
3) 96_32 = 64 شخصا. - الغناء في الجوقة؛
4) 96 - 78 = 18 فرداً. - القيام بالرقص؛
5) 96 - 82 = 14 فرداً. - ممارسة الجمباز الإيقاعي.
1) 82-32 = 50 فرداً. - عدد الطلاب الذين يغنون في الجوقة أكبر بكثير من عدد الطلاب الذين يغنون في الجمباز الإيقاعي؛
2) 50+78=128 شخص. - مضاعفة عدد الطلاب الذين يغنون في الجوقة؛
3) 128÷2 = 64 شخصًا. - الغناء في الجوقة؛
4) 78 - 64 = 14 فرداً. - ممارسة الجمباز الإيقاعي؛
5) 82-64 = 18 فرداً. - يشاركون في الرقص.
الإجابة: 64 طالبًا يغنون في جوقة؛ 14 طالبًا يمارسون الجمباز الإيقاعي. 18 طالبًا يرقصون.
الطريقة الجبرية. حل مشكلة باستخدام الطريقة الجبرية يعني إيجاد الإجابة على متطلبات المشكلة من خلال تكوين وحل معادلة أو نظام المعادلات. يمكن أيضًا حل نفس المشكلة بطرق جبرية مختلفة، إذا تم تجميع معادلات أو أنظمة معادلات مختلفة لحلها، والتي يكون أساسها علاقات مختلفة بين البيانات والبيانات المطلوبة.
مثال. يمكن للعامل أن يصنع عددًا معينًا من الأجزاء في ثلاثة أيام. إذا قام بصنع 10 أجزاء إضافية في اليوم، فيمكنه إكمال المهمة في يومين. ما هي الإنتاجية الأولية للعامل وكم عدد الأجزاء التي يجب أن يصنعها؟
1 الطريق. اجعل x d./day هي الإنتاجية الأولية للعامل. إذن (x+10) d./day هي الإنتاجية الجديدة، 3x d هو عدد الأجزاء التي يجب عليه تصنيعها. بالشرط نحصل على المعادلة 3س=2(+10)، وحلها نجد س=20. الإنتاجية الأولية للعامل هي 20 جزءًا في اليوم، وعليه أن يصنع 60 جزءًا.
الطريقة 2. دع x d هو عدد الأجزاء التي يجب على العامل صنعها. إذن x/2 يوم/يوم هي الإنتاجية الجديدة، (x/2-10) يوم/يوم هي الإنتاجية الأصلية للعامل. بالشرط نحصل على المعادلة x=3(x/2-10) وحلها نجد x=60. يجب على العامل أن يصنع 60 جزءًا، وتكون إنتاجيته الأولية 20 جزءًا في اليوم.
الجواب: 20 جزءًا في اليوم، 60 جزءًا.
الطريقة الهندسية. حل مشكلة باستخدام الطريقة الهندسية يعني إيجاد إجابة لمتطلبات المشكلة باستخدام الإنشاءات الهندسية أو خصائص الأشكال الهندسية. يمكن أيضًا حل نفس المشكلة بطرق هندسية مختلفة. تعتبر المشكلة محلولة بطرق مختلفة إذا تم استخدام هياكل أو خصائص مختلفة لتكوينها.
الطريقة المنطقية. حل المشكلة باستخدام الطريقة المنطقية يعني العثور على إجابة لمتطلبات المشكلة، كقاعدة عامة، دون إجراء حسابات، ولكن فقط باستخدام التفكير المنطقي. ومن أمثلة هذه المسائل مسائل "العبور"، ومثالها الكلاسيكي مسألة الذئب والماعز والملفوف، أو مسائل "الوزن".
طريقة عملية. حل مشكلة باستخدام أسلوب عملي يعني العثور على إجابة لمتطلبات المشكلة عن طريق تنفيذ إجراءات عملية مع الكائنات أو نسخها (النماذج، والتخطيطات، وما إلى ذلك)
لأن موضوع دوراتنا هو حل المشكلات النصية باستخدام الطريقة الجبرية، وسننظر في ذلك بمزيد من التفصيل.
إن الطريقة الجبرية لحل المسائل تجعل من السهل إظهار أن بعض المسائل، التي تختلف عن بعضها البعض فقط في الحبكة، ليس لها نفس العلاقات بين البيانات والكميات المطلوبة فحسب، بل تؤدي أيضًا إلى تفكير نموذجي يتم من خلاله تحديد هذه العلاقات. مقرر. توفر مثل هذه المشكلات فقط تفسيرات محددة مختلفة لنفس المنطق الرياضي، ونفس العلاقات، أي. لديهم نفس النموذج الرياضي.
دعونا ننظر في تصنيف المسائل التي تم حلها جبريا عن طريق الرسم، وذلك بسبب تنوع المعادلات والمتباينات.
مهام الحركة
تتضمن هذه المجموعة من المسائل مسائل تتناول ثلاث كميات: المسار والسرعة والزمن. وكقاعدة عامة، فإنها تتعامل مع حركة خطية موحدة. من المفيد جدًا في هذه المسائل رسم رسم توضيحي يساعد في تكوين المعادلات والمتباينات.
يمكن تقسيم هذه المجموعة من المهام إلى مهام يتم فيها مراعاة حركات الأجسام: 1) تجاه بعضها البعض، 2) في اتجاه واحد ("المطاردة")، 3) في اتجاهين متعاكسين، 4) على طول مسار مغلق، 5) على امتداد النهر.
مهام للعمل.
تتضمن هذه المجموعة من المهام مهام تتحدث عن ثلاث كميات: العمل، الوقت الذي يتم خلاله تنفيذ العمل، الإنتاجية - العمل المنتج لكل وحدة زمنية. وتشمل مهام العمل أيضًا المهام المتعلقة بملء وتفريغ الخزانات باستخدام الأنابيب والمضخات والأجهزة الأخرى. في هذه الحالة، يعتبر حجم المياه التي يتم ضخها بمثابة العمل المنجز.
يمكن تصنيف مهام العمل على أنها مهام حركية، لأن في مشاكل من هذا النوع، يمكننا أن نفترض أن العمل بأكمله أو الحجم الإجمالي للخزان يلعب دور المسافة، وأداء الكائنات التي تقوم بالعمل يشبه سرعة الحركة. ومع ذلك، من حيث المؤامرة والمؤامرة، فإن هذه المهام مختلفة تماما.
مسائل على المخاليط والنسب المئوية.
تتضمن هذه المجموعة من المسائل مسائل تتعلق بخلط مواد مختلفة بنسب معينة، بالإضافة إلى مسائل تتعلق بالنسب المئوية.
لقد نظرنا في بعض تصنيفات المشكلات، والآن نود أن ننظر بمزيد من التفصيل في حل المشكلات باستخدام النمذجة الرياضية.
§3. حل المشكلات من خلال تسليط الضوء على 3 مراحل للنمذجة الرياضية
يختلف علماء الرياضيات عن بعضهم البعض في أنهم يتحدثون مع بعضهم البعض ويكتبون "بلغة رياضية" خاصة. باستخدام اللغة الرياضية، يمكنك إنشاء نماذج رياضية لمواقف حقيقية. في عملية حل المشكلة، يتم تمييز ثلاث مراحل من النمذجة الرياضية: 1) وضع نموذج رياضي، 2) العمل مع نموذج رياضي، 3) الإجابة على سؤال المشكلة. دعونا نلقي نظرة على بعض الأمثلة التي تناقش مراحل النمذجة الرياضية.
سار السائح لمدة ساعتين من النقطة أ إلى النقطة ب، ثم عند النقطة ب استقل قاربًا تبلغ سرعته 4 أضعاف سرعة السائح كمشاة، وركب القارب لمدة ساعة ونصف إلى النقطة ج. استقل حافلة تبلغ سرعتها ضعف سرعة القارب، وركب عليها لمدة ساعتين حتى النقطة د. ما هي السرعة التي سافر بها السائح في الحافلة إذا علم أن طريقه بالكامل من أ إلى D كان 120 كم؟