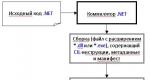
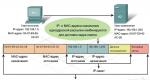
Transformada de Fourier en electrónica de potencia. Serie de Fourier Armónico cero en la expansión de la serie de Fourier
Comencemos con un circuito simple para cubrir los conceptos básicos que luego usaremos para circuitos más complejos. En la fig. 7.1 muestra el voltaje de entrada V BX.p = 1 V, esta es una onda sinusoidal con una frecuencia F\u003d 1 kHz y un valor máximo de 1 V (rms V en=√2). Para proporcionar una tensión de salida que sea una función no lineal de la tensión de entrada, se utiliza como amplificador una fuente de tensión controlada por tensión E (VUNC). En este ejemplo, la dependencia del voltaje de salida con respecto a la entrada se muestra mediante la función
F(X) = 1 + X + X².
Arroz. 7.1. Esquema con una relación no lineal entre los voltajes de entrada y salida
Esta relación funcional se muestra en el comando E usando coeficientes polinómicos. Vista general del polinomio:
F(X) = k 0 + k 1 X + k 2 X².
Para llegar a nuestra dependencia de ejemplo, usamos los últimos tres números del comando de entrada E. Queremos hacer un análisis de armónicos para ver qué armónicos están presentes en el voltaje de salida, pero primero tratemos de determinar qué debemos esperar.
Antes de proceder a la expansión de las dependencias temporales en una serie de Fourier, es necesario realizar un análisis para procesos transitorios (programa de análisis transitorio en PSpice).
Por lo tanto, se deben usar los comandos .TRAN y .FOUR. Por lo general, se realiza un análisis transitorio para un período completo de la frecuencia fundamental. En este ejemplo F=1kHz; Como consecuencia, T=1/F= 1 ms. El análisis armónico refleja los componentes de frecuencia hasta el noveno armónico. Para la mayoría de los propósitos, esto debería ser más que suficiente. Si se muestran armónicos más altos, no importarán mucho debido a la acumulación de errores de redondeo en los resultados.
Para dar una descripción más detallada del voltaje de entrada VBX, utiliza el formulario pecado para describir la fuente. Parámetros sin( a, b,Con,…) significar: a- componente constante, b- valor máximo, Con- frecuencia, d- demora, mi- coeficiente de atenuación y F- fase.
Cuando se incluye en el archivo de entrada, el comando .FOUR produce un análisis armónico que produce una expansión de Fourier de los resultados del análisis transitorio. Los parámetros para este comando incluyen la frecuencia fundamental y las variables para las cuales se obtendrá la expansión. En este ejemplo, estas variables serán funciones periódicas de los voltajes de entrada V(1) y salida V(2). Fichero de entrada:
Vin 1 0 sin(0 1 1000); argumentos para desplazamiento, máximo y frecuencia
E 2 0 poli(1) 1,0 1 1 1; últimos 3 valores para k0, k1, k2
Realice el análisis, luego obtenga las gráficas V(1) y (V)2. Asegúrese de que V(1) sea una copia exacta del voltaje de entrada V VX. El voltaje de salida debe mostrar un componente de CC y una onda compleja con un máximo de 3 V. A partir de un estudio teórico de la serie de Fourier, se puede concluir que este gráfico se asemeja a una onda periódica que consta de la fundamental y la segunda armónica. Es recomendable imprimir una copia de este gráfico para un estudio futuro. En la fig. 7.2 muestra estos gráficos.

Arroz. 7.2. Gráficos de tensión v 1 y v 2 para el circuito de la fig. 7.1
Considere también el archivo de salida para este circuito (Figura 7.3), que muestra los siguientes valores para los voltajes de los nodos: V(1)=0 V y V(2)=1 V. Esto significa que aunque la señal de entrada no tiene offset, la salida de tensión tiene un offset V(2)=1V.
En la fig. 7.3 en la tabla de componentes de la serie de Fourier para V(1), no todos los componentes tienen valores reales. Así, el valor del componente constante teóricamente debería ser igual a cero, pero el análisis da un valor muy pequeño de 3.5E-10, que no es exactamente igual a cero debido a la acumulación de errores de redondeo.
Análisis de Fourier; Descomposición de Polinomio
Vin 1 0 sin(0 1 1000); los argumentos son compensación, pico y frecuencia
E 2 0 poli(1) 1,0 1 1 1; los últimos 3 1 son para k0, k1, k2
2 2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01
5 5.000E+03 3.134E-09 3.134E-09 -9.107E+01 -9.107E+01
6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01
ARMÓNICA FRECUENCIA FOURIER NORMALIZADA FASE NORMALIZADA
NO (HZ) COMPONENTE COMPONENTE (GRADOS) FASE (GRADOS)
1 1.000E+03 1.000E+00 1.000E+00 -2.888E-07 0.000E+00
2 2.000E+03 5.000E-01 5.000E-01 -9.000E+01 -9.000E+01
3 3.000E+03 7.971E-08 7.971E-08 -1.546E+02 -1.546E+02
4 4.000E+03 5.126E-08 5.126E-08 -1.439E+02 -1.439E+02
5 5.000E+03 3.918E-08 3.918E-08 -1.420E+02 -1.420E+02
6 6.000E+03 3.327E-08 3.327E-08 -1.299E+02 -1.299E+02
7 7.000E+03 3.606E-08 3.606E-08 -1.268E+02 -1.268E+02
8 8.000E+03 2.889E-08 2.859E-08 -1.316E+02 -1.316E+02
9 9.000E+03 2.584E-08 2.584E-08 -1.189E+02 -1.189E+02
DISTORSIÓN ARMÓNICA TOTAL = 4.999939E+01 POR CIENTO
Arroz. 7.3. El archivo de salida con los resultados del análisis del circuito en la fig. 7.1
El primer armónico es el armónico fundamental en F=1kHz. Se muestra la amplitud del primer armónico de la serie de Fourier y su fase 2,4Å-7 (también casi cero). Si asumimos que este componente se expresa mediante la fórmula
segundo norte pecado( nx),
entonces esto significa que b 1 =1, norte=1, donde el índice 1 corresponde a la frecuencia fundamental. Se pueden ignorar otros armónicos, ya que sus amplitudes son muchos órdenes de magnitud más pequeñas que el armónico fundamental. Es el armónico fundamental que se refleja en el gráfico V(1) en Probe, obtenido a partir de los datos de la Fig. 7.3.
Otra tabla de componentes de Fourier en la fig. 7.3 se refiere a V(2). Al observar los distintos armónicos, tenga en cuenta que hay un componente de CC de 1,5 V. ¿Por qué 1,5 V? Componente k 0 = 1 V da solo una parte de este valor, los 0,5 V restantes están asociados con el segundo armónico. La teoría muestra que con distorsión armónica en el segundo armónico en el voltaje de salida, además del segundo armónico en sí mismo con amplitud b 2, aparece una componente constante asociada a distorsiones en el segundo armónico con el valor b 0 =b 2. La amplitud de la frecuencia fundamental en la expansión es b 1 \u003d 1 V, amplitud del segundo armónico b 2 =0,5 V, su ángulo de fase es -90°. Los armónicos más altos son mucho más pequeños y se pueden ignorar.
Como ejercicio de síntesis armónica, puede dibujar los armónicos individuales y sumarlos para predecir el resultado que obtendrá en Probe for V(2). Recuerde tener en cuenta la componente continua y las correspondientes amplitudes y fases para la fundamental y la segunda armónica. Una vez que haya dibujado la forma de onda resultante, sin duda le complacerá saber que PSpice puede hacer el tedioso trabajo por usted.
Adición de armónicos y descomposición en componentes armónicos
Vamos a crear un nuevo archivo de entrada correspondiente a la Fig. 7.4, en el que al diagrama de la Fig. 7.1, se añaden dos fuentes de corriente independientes más.
Usamos dos fuentes solo para que pueda obtener los armónicos fundamentales y segundos en el mismo gráfico con el voltaje de salida. Las fuentes adicionales alimentan una resistencia de 1 ohm conectada en paralelo. Tal cambio en el esquema original no es necesario en absoluto, simplemente resultó ser conveniente con un conjunto dado de parámetros. El nuevo archivo de entrada es una extensión del archivo anterior y se ve así:
Análisis de Fourier; Descomposición de Polinomio
Vin 1 0 sin(0 1 1000); argumentos - compensación, amplitud y frecuencia
E 2 0 poli(1) 1,0 1 1 1; últimos 3 registros para k0, k1, k2
i2 0 3 sin(0.5 0.5 2000 0 0 -90)

Arroz. 7.4. Esquema para analizar la suma de armónicos y expansión en una serie de Fourier
Antes de realizar el análisis, echemos un vistazo más de cerca a las descripciones de i 1 y i 2. Para la síntesis armónica se utilizan los resultados de la expansión en serie de Fourier del problema anterior. Asegúrese de comprender el significado de todos los parámetros; luego ejecute el análisis en Probe para obtener gráficos I(i1), I(i2) e I(r). Aunque son corrientes, son numéricamente iguales a los voltajes, ya que pasan por una resistencia de 1 ohm. En la fig. 7.5 presenta los resultados. Ahora puedes establecer que la primera gráfica es el armónico fundamental, la segunda es el segundo armónico y la tercera es el resultado de sumarlas en una resistencia r. Por supuesto, puede obtener una gráfica de V(3) en lugar de I(r). Al mismo tiempo, el eje Y se etiquetarán en unidades de voltaje, no de corriente. Verifique que la suma de las dos primeras curvas da la tercera curva en diferentes puntos en el tiempo. Para hacer el gráfico más compacto, usamos un desplazamiento de 1V para el fundamental y 0.5V para el segundo armónico. De hecho, el armónico fundamental tiene desplazamiento cero.

Arroz. 7.5. Los armónicos fundamental y segundo y el resultado de su suma
Distorsión de segundo armónico en amplificadores
Cuando el área de operación del amplificador va más allá de la parte lineal de la característica, esto genera cierta distorsión. La primera aproximación a la curva de salida real se logra al incluir el segundo armónico en el modelo, mostrando que la función de transición que conecta yo c y yo b(corriente de colector y base) es una especie de parábola. Por lo general, la distorsión es mucho menor que la supuesta en nuestro primer ejemplo introductorio, que se muestra en la Fig. 7.1. Un polinomio más exacto viene dado por la fórmula
F(X) = 0,1 + X + 0,2X².
Es suficiente simplemente transformar el archivo de entrada original para reflejar esta situación. Comando de entrada para fuente dependiente mi tomará la forma:
E20 poli(1) 1,0 0,1 1 0,2; últimos tres valores para k0, k1, k2
y todo el archivo de entrada será:
Ejecute el análisis y obtenga gráficos V(1) y V(2) en Probe. Verás que ambas ondas parecen ondas sinusoidales reales. Para una comparación más precisa, elimine la gráfica V(2) y obtenga una gráfica V(2)–0.1 en su lugar. Esto acercará ambas curvas. Al comparar ondas, recuerde que V(1) es solo una onda sinusoidal y V(2) es una combinación de armónicos fundamentales y segundos. En este ejemplo, el segundo armónico tiene una amplitud mucho menor que en el anterior. Puede imprimir los resultados del estudio que se muestra en la fig. 7.6.

Arroz. 7.6. Los armónicos fundamental y segundo y el resultado de su suma
Después de salir del programa Probe, considere el archivo de salida para este caso. El voltaje de entrada V(1) es exactamente el mismo que en el ejemplo anterior, pero por supuesto que V(2) es diferente. Tenga en cuenta que el componente de CC del voltaje de salida es de 0,2 V y el segundo armónico en F=2 kHz tiene una amplitud de 0,1 V y un ángulo de fase de -90°. Otros armónicos son mucho más pequeños y pueden despreciarse. Finalmente, determine la distorsión armónica total, que es muy cercana al 10%, como se esperaba. La distorsión del segundo armónico se define como b 1 /b 2 donde b 1 y b 2 - coeficientes en los armónicos segundo y fundamental, respectivamente. Estos datos se muestran en la fig. 7.7.
Análisis de Fourier; Segunda distorsión armónica, amplificador de potencia
TENSIÓN DE NODO TENSIÓN DE NODO TENSIÓN DE NODO TENSIÓN DE NODO
COMPONENTES DE FOURIER DE LA RESPUESTA TRANSITORIA V(1)
ARMÓNICA FRECUENCIA FOURIER NORMALIZADA FASE NORMALIZADA
NO (HZ) COMPONENTE COMPONENTE (GRADOS) FASE (GRADOS)
1 1.000E+03 1.000E+00 1.000E+00 1.115E-06 0.000E+00
2 2.000E+03 1.994E-08 1.994E-08 -9.308E+01 -9.308E+01
3 3.000E+03 7.381E-09 7.381E-09 -9.083E+01 -9.083E+01
4 4.000E+03 4.388E-09 4.388E-09 -8.993E+01 -8.993E+01
5 5.000E+03 3.134E-09 3.134E-09 -9.107E+01 -9.107E+01
6 6.000E+03 1.525E-09 1.525E-09 -6.706E+01 -6.706E+01
7 7.000E+03 1.511E-09 1.511E-09 -1.392E+02 -1.392E+02
8 8.000E+03 1.237E-09 1.237E-09 -3.990E+01 -3.990E+01
9 9.000E+03 7.642E-10 7.642E-10 3.320E+01 3.320E+01
DISTORSIÓN ARMÓNICA TOTAL = 2.208405E-06 POR CIENTO
COMPONENTES DE FOURIER DE LA RESPUESTA TRANSITORIA V(2)
ARMÓNICA FRECUENCIA FOURIER NORMALIZADA FASE NORMALIZADA
NO (HZ) COMPONENTE COMPONENTE (GRADOS) FASE (GRADOS)
1 3.000E+03 1.000E+00 1.000E+00 7.683E-07 0.000E+00
2 2.000E+03 1.000E-01 1.000E-01 -9.000E+01 -9.000E+01
3 3.000E+03 1.756E-08 1.756E-08 -1.336E+02 -1.336E+02
4 4.000E+03 1.430E-08 1.430E-08 -1.348E+02 -1.348E+02
5 5.000E+03 9.547E-09 9.547E-09 -1.365E+02 -1.365E+02
6 6.000E+03 8.100E-09 8.100E-09 -1.232E+02 -1.232E+02
7 7.000E+03 6.463E-09 6.463E-09 -1.342E+02 -1.342E+02
8 8.000E+03 5.743E-09 5.743E-09 -9.544E+01 -9.544E+01
9 9.000E+03 6.931E-09 6.931E-09 -1.092E+02 -1.092E+02
DISTORSIÓN ARMÓNICA TOTAL = 9.999880E+00 POR CIENTO
Arroz. 7.7. Los resultados del análisis de la distorsión del segundo armónico en amplificadores.
Distorsión de intermodulación
Usamos un circuito simple (fig. 7.8) para mostrar cómo se combinan dos ondas sinusoidales en un dispositivo no lineal que usa frecuencias bastante cercanas entre sí, a saber F 1 = 1kHz y F 2 = 1,5kHz. La mezcla no lineal tiene lugar en la fuente dependiente del tipo e VCVS (INUN). El polinomio que describe la relación tiene más términos que en el ejemplo anterior:
F(X) = 1 + X + X² + X³.

Arroz. 7.8. Circuito para demostrar la distorsión de intermodulación
Las corrientes, en suma, crean en R= 1 Ω voltaje V(1), numéricamente igual a la corriente en r Por lo tanto, el voltaje de entrada V(1) puede considerarse como el voltaje en un mezclador no lineal. Dado que las ondas sinusoidales tienen diferentes frecuencias, su suma es una oscilación periódica compleja con una frecuencia diferente de la frecuencia de los componentes originales (frecuencia de pulsación). Fichero de entrada:
Ejecute la simulación y acceda a la sonda V(1). Seleccione Gráfico, Configuración del eje X..., Definido por el usuario y configure el rango de 0 a 10 ms para lograr un voltaje de entrada constante. Este gráfico se muestra en la Fig. 7.9. Para confirmar que en realidad es la suma de los armónicos de 1 y 1,5 kHz, seleccionamos Trace, Fourier, pasando del dominio del tiempo al dominio de la frecuencia. Cambiemos los bordes a lo largo del eje. X ajustando el rango de frecuencia de 4 a 12 kHz. Asegúrese de que los parámetros del eje correspondan a las frecuencias deseadas y las amplitudes esperadas. De hecho, cuando F\u003d 1 kHz, el voltaje es 0.991 V, y en F= 1,5 kHz es 0,979 V. Tenga en cuenta que hay algún error de acumulación con esta síntesis. En la fig. 7.10 muestra la respuesta de frecuencia correspondiente.

Arroz. 7.9. Tensión de salida con distorsión de intermodulación

Arroz. 7.10. Composición espectral de la tensión de entrada
Luego seleccione Trace, End Fourier para volver al dominio del tiempo, elimine el gráfico V(1) y obtenga el voltaje de salida del mezclador V(2). Recuerde que el mezclador es un INUN con una conexión polinomial dada por la función F(X). La dependencia del tiempo es un gráfico similar al gráfico V(1), pero una mirada más cercana revela que las formas de tensión son significativamente diferentes. Se pueden obtener algunas pistas del contenido armónico de esta forma de onda compleja, por lo que será necesario volver al dominio de la frecuencia seleccionando un rango a lo largo del eje X de 0 a 5 kHz. Recomendamos imprimir el espectro de frecuencias para su posterior estudio. El análisis teórico de los componentes de modulación de frecuencia le permite predecir y verificar los resultados del análisis en PSpice. Tenga en cuenta que hay un componente de 2 V CC junto con componentes significativos en el rango de 0,5 a 4,5 kHz (consulte la Figura 7.11 para ver el espectro de frecuencia).

Arroz. 7.11. Composición espectral de la tensión de salida
Adición de armónicos
El caso más simple para el análisis teórico es el caso de un efecto armónico en un circuito que consta de componentes lineales como resistencias, condensadores e inductores y, como sabe, la respuesta es una oscilación armónica a la misma frecuencia de la señal de entrada. Diferentes caídas de voltaje en el circuito también son oscilaciones armónicas con la misma frecuencia, que difieren solo en amplitud y fase. Usemos un diagrama simple para ilustrar algunas de estas propiedades. En la fig. 7.12 muestra tres fuentes de tensión que alimentan un circuito que contiene resistencias R= 1 ohmio y R 1 =R 2 \u003d 0,001 ohmios. Las dos últimas resistencias son necesarias para que las fuentes de voltaje no sean ideales. Usando este diagrama, podemos mostrar la adición de ondas sinusoidales en Probe. Fichero de entrada:
Adición de ondas sinusoidales de la misma frecuencia
*El orden de los parámetros en una expresión compleja para armónicos
*componentes: compensación, amplitud, frecuencia, retardo, atenuación, fase
v2 2 0 sen(0 1 1kHz 0 0 45); fase=45 grados
v3 3 0 sin(0 1 1kHz 0 0 90); fase=90 grados

Arroz. 7.12. Esquema para agregar señales armónicas de una frecuencia.
Ejecute la simulación y los gráficos de sonda v(1), v(2) y v=v(1)+v(2). Los gráficos resultantes muestran el voltaje v 2 con un retraso máximo de aproximadamente 45° desde el máximo v 1, y el voltaje total v 1 +v 2 con un máximo situado entre sus valores máximos. Asegúrese de que el máximo v 1 = 1 V alcanzado a 251 µs (90°), máximo v 2 \u003d 1 V - en el momento de 131 μs (47,16 °) y máximo v 1 +v 2 \u003d 1.8381 V - en el momento de 171 μs (61.56 °). Elimine estos gráficos y obtenga dependencias temporales para otras combinaciones de voltajes, por ejemplo, para v(1), v(3) y v(1)+v(3). En función de su capacidad para agregar vectores de tensión, intente predecir el valor de amplitud para la suma de las tensiones antes de obtener los gráficos de la sonda que se muestran en la Figura 2. 7.13.

Arroz. 7.13. El resultado de la suma de señales armónicas de la misma frecuencia.
Adición de armónicos fundamentales y segundos
En el archivo de entrada correspondiente al esquema de la Fig. 7.12, puede variar fácilmente los parámetros y la composición de las fuentes de alimentación. vamos a borrar v 3 y duplicar la frecuencia de voltaje v 2 para convertirse en la segunda frecuencia armónica para v una . Por supuesto, la oscilación resultante se volverá inmediatamente no sinusoidal. De hecho, su forma dependerá de la relación de los ángulos de fase v 1 y v 2. Deje que ambos armónicos alcancen su máximo simultáneamente en el ejemplo considerado. Archivo de entrada para este caso:
Adición de ondas sinusoidales; Pico fundamental y de segundo armónico juntos
Ejecute la simulación y trace v(1), v(2) y v=v(1)+v(2) en Probe. Porque el v 1 y v 2 pico al mismo tiempo, el máximo de oscilación resultante es de 2 V, pero cuando la fundamental alcanza un máximo negativo, el segundo armónico vuelve a un máximo positivo, y su suma se vuelve cero. Es claro que la fluctuación total ( v 1 +v 2) no sinusoidal. Estos gráficos se muestran en la fig. 7.14.

Arroz. 7.14. El resultado de sumar el primer y segundo armónico
Amplitud modulada
Se puede obtener un gráfico interesante de una forma de onda modulada en amplitud en PSpice usando la función de multiplicación de oscilaciones armónicas con frecuencias significativamente diferentes. En la fig. 7.15 muestra un circuito que simula tal dispositivo. La fuente del primer armónico es v 1 con una frecuencia de 1 kHz. segundo origen v 2 tiene una frecuencia de 20 kHz. La multiplicación se realiza en la fuente dependiente e, que es el INUN (VCVS). Se necesitan resistencias para evitar potenciales flotantes. Fichero de entrada:
e 3 0 poli(2) 1.0 2.0 0 0 0 0 1

Arroz. 7.15. Multiplicador para modulación de onda sinusoidal
Las últimas cinco entradas en el comando de entrada de fuente polinomial son: 0 0 0 0 1. Recuerde que estos son los valores de los coeficientes en los términos k 0 , k 1 v 1 , k 2 v 2 , k 3 v 12 y k 4 v 1 v 2. Todos los valores son 0 excepto k 4 , que es igual a 1.
Ejecute la simulación y obtenga gráficas de v(1) y v(3) en Probe. El componente armónico con una frecuencia de 20 kHz no se construye deliberadamente sobre el gráfico general, para no complicar la comprensión de los procesos. La oscilación resultante v(3) tiene la forma clásica de una oscilación modulada en amplitud. En este ejemplo, ambos armónicos de entrada v 1 y v 2 tienen una amplitud de 1 V. Los gráficos se muestran en la fig. 7.16.

Arroz. 7.16. El resultado del estudio de las señales moduladas en amplitud.
Mientras aún está en Probe, agregue otro voltaje de entrada v(2) trazado para mostrar todos los voltajes: v(1), v(2) y v(3). Ahora bien, este gráfico contiene, junto con las otras dos ondas, la portadora, dando la imagen completa. Obtenga una copia impresa para estudiarla más a fondo, luego elimine la gráfica v(2) y seleccione Trace, Fourier. Instalar a lo largo del eje X límites de rango de 0 a 30 kHz. El dominio de frecuencia ahora muestra componentes de 1,19 kHz y 21 kHz. Los últimos componentes son las frecuencias laterales superior e inferior resultantes de esta modulación. Determine la amplitud de cada una de estas ondas. Recuerda la identidad trigonométrica,
(pecado a)(pecado b) = 0.5,
lo que explica las amplitudes de 0,5 V para las frecuencias de banda lateral. Consulte la fig. 7.17, que muestra el espectro de frecuencias. (Se han eliminado los marcadores para una imagen más clara). Analice con diferentes amplitudes relativas para el voltaje de modulación v 1 para ver qué efecto tiene esto en la profundidad de modulación t. por ejemplo, cuando v 1 tiene una amplitud de 0,8, ¿cuál es la profundidad de modulación y cómo se ve la oscilación resultante?

Arroz. 7.17. Espectro de frecuencia de una oscilación modulada en amplitud
Una descripción general de los nuevos comandos de PSpice utilizados en este capítulo
.CUATRO <частота>*<выходные переменные>
Por ejemplo, la entrada
muestra que se está realizando una expansión de Fourier. La descomposición solo se puede realizar después de obtener la dependencia del tiempo para el estado estacionario obtenido del análisis transitorio. Tal comando debe estar presente en el archivo de entrada:
TRAN <шаг><момент окончания>
Tareas
El análisis de armónicos proporciona el componente de CC de la fundamental y todos los armónicos hasta el noveno inclusive. Sus amplitudes y fases se muestran con valores reales y relativos. En el ejemplo anterior, se analizaron V(1) y V(2) y sus componentes. Usualmente, para realizar un análisis armónico, se usa el comando .INVESTIGACION: sin embargo, los comandos también se pueden usar en su lugar .IMPRESIÓN o .GRÁFICO.
7.1. En la fig. 7.18 el polinomio para E tiene la forma
F(X) = X + X².

Arroz. 7.18
Usando pico= 1 V, F=1kHz y V = 1 Comparar v 0 yo. Prediga el contenido armónico aproximado del voltaje de salida; luego realice un análisis en PSpice que mostrará el contenido armónico de los voltajes de entrada y salida. En el comando .FOUR, use los voltajes V(2, 1) y V(3). Examine el archivo de salida y determine el contenido armónico de V(3).
7.2. En el Problema 7.1, use Trace, Fourier para obtener el contenido armónico de V(3). Visualización de V(2,1) y V(3), establecer el eje X límites de 0 a 5 kHz.
7.3. Realice el análisis del problema 7.1 con
F(X) = 2 + 0,1X².
Prediga el contenido armónico aproximado del voltaje de salida; luego trace V(2,1) y V(3) para verificar la precisión de sus predicciones.
7.4. En la fig. 7.4 muestra una fuente polinomial E. Se dio como
F(X) = 1 + X + X².
Cambia el polinomio a
F(X) = X + X²,
y realizar síntesis y descomposición cambiando i 1 y i 2 para que la corriente I(r) siga la forma del voltaje V(2).
7.5. En la sección "Segunda distorsión armónica en amplificadores" de este capítulo, reemplace el polinomio con lo siguiente:
F(X) = 0,05 + X + 0,1X²,
y ejecute el análisis en PSpice como se sugiere en el texto. Obtenga una gráfica de V(1) y (V)2-0.05 para comparar los voltajes de entrada y salida variables. Predecir los valores de la componente DC de la tensión de salida, amplitud y fase del segundo armónico y distorsión armónica total. Pruebe sus predicciones con los resultados de Probe y el archivo de salida.
7.6. En la sección de distorsión de intermodulación, combinamos dos ondas sinusoidales de diferentes frecuencias. Realizar análisis a frecuencias F 1 = 2kHz y F 2 = 2,5 kHz, dejando la expresión para F(X) sin cambios. Modifique el comando .TRAN según la tarea. Siga los pasos en el mismo orden que en el ejemplo de texto para probar sus predicciones sobre el contenido armónico del voltaje de salida.
7.7. En la sección "Adición de armónicos" en la fig. 7.12 muestra ramas paralelas con tres fuentes de voltaje. La adición de armónicos fue más matemática que física. Cambie el circuito para que todas las fuentes de voltaje estén conectadas en serie, luego vuelva a ejecutar el análisis. ¿Obtuviste los mismos resultados?
7.8. Realice un análisis para agregar los siguientes voltajes armónicos de frecuencia única F=1kHz:
v 1 = 0,5∠0°V, v 2 =1∠45°V y v 23 =1.5∠90° V.
Donde:
a) Encuentre el valor máximo ( v 1 +v 2), así como el tiempo y el ángulo de fase en el que se alcanza el máximo.
b) Repita el paso a) para ( v 1 +v 3).
Cuando use el modo de cursor y múltiples gráficos en la misma pantalla, use el botón [ control] y las flechas ← y → para seleccionar en cuál de los gráficos debe moverse el cursor.
7.9. Para ilustrar el efecto de sumar armónicos con frecuencias cercanas, realice el análisis como en el problema 7.8 para el siguiente conjunto de parámetros: v 1 =1∠0° V, F 1 = 1kHz, v 1 =1∠0° V, F 2 \u003d 1,2 kHz, v 1 =1∠0° V y F 3=1,4kHz:
a) Obtener los gráficos v 1 , v 2 y ( v 1 +v 2). Encuentre el valor máximo ( v 1 +v 2).
b) Obtener gráficos v 1 , v 3 y ( v 1 +v 3). Encuentre el valor máximo ( v 1 +v 3).
7.10. Resuelva el problema de la sección sobre modulación de amplitud configurando v 1 = 1 V a 1 kHz, y cambiando v 1 para que la profundidad de modulación sea 0,5. Ejecute el análisis en PSpice para mostrar sus resultados.
La transformada de Fourier es el medio más utilizado para convertir una función arbitraria del tiempo en un conjunto de sus componentes de frecuencia en el plano de números complejos. Esta transformación se puede aplicar a funciones aperiódicas para determinar sus espectros, en cuyo caso el operador complejo s se puede reemplazar por /co:
Para determinar las frecuencias más interesantes se puede utilizar la integración numérica en el plano complejo.
Para familiarizarse con los conceptos básicos del comportamiento de estas integrales, consideramos varios ejemplos. en la fig. 14.6 (izquierda) muestra el pulso de área unitaria en el dominio del tiempo y su composición espectral; en el centro, un pulso de la misma área, pero de mayor amplitud, ya la derecha, la amplitud del pulso es infinita, pero su área sigue siendo igual a la unidad. La imagen de la derecha es especialmente interesante porque el espectro de pulsos de ancho cero contiene todas las frecuencias con amplitudes iguales.

Arroz. 14.6. Espectros de pulsos del mismo ancho, a lo largo del mismo piaosrdi
En 1822 el matemático francés J. B. J. Fourier (J. B. J. Fourier) demostró en su trabajo sobre conductividad térmica que cualquier función periódica se puede descomponer en componentes iniciales, incluida la frecuencia de repetición y un conjunto de armónicos de esta frecuencia, y cada uno de los armónicos tiene su propia amplitud y fase con respecto a la tasa de repetición. Las fórmulas básicas utilizadas en la transformada de Fourier son:
![]()
![]()


donde A() es la componente continua, y A p y B p son armónicos de la frecuencia fundamental de orden y, respectivamente, en fase y antifase con ella. La función f(*) es pues la suma de estos armónicos y Lo-
En los casos en que f(x) es simétrica con respecto a mc/2, es decir, e. f(x) en la región de n a 2n = -f(x) en la región de 0 a n, y no hay componente DC, las fórmulas de la transformada de Fourier se simplifican a:

donde n = 1, 3.5, 7…
Todos los armónicos son sinusoides, solo algunos de ellos están en fase y algunos están desfasados con la frecuencia fundamental. La mayoría de las formas de onda que se encuentran en la electrónica de potencia se pueden descomponer en armónicos de esta manera.
Si se aplica la transformada de Fourier a pulsos rectangulares con una duración de 120°, entonces los armónicos serán un conjunto de orden k = bi ± 1, donde n es uno de los números enteros. La amplitud de cada armónico h con respecto al primero está relacionada con su número por la relación h = l//e. En este caso, el primer armónico tendrá una amplitud 1,1 veces mayor que la amplitud de una señal rectangular.
La transformada de Fourier da el valor de amplitud de cada armónico, pero como todos son sinusoidales, el valor rms se obtiene simplemente dividiendo la amplitud correspondiente por la raíz de 2. El valor rms de una señal compleja es la raíz cuadrada de la suma de los cuadrados de los valores rms de cada armónico, incluido el primero.
Cuando se trata de funciones de impulsos repetitivos, es útil considerar el ciclo de trabajo. Si los pulsos repetidos en la Fig. 14.7 tiene un valor rms X en el tiempo A, entonces el valor rms en el tiempo B será X(A/B) 1 2 . Por lo tanto, el valor RMS de los pulsos repetitivos es proporcional a la raíz cuadrada del valor del ciclo de trabajo. Aplicando este principio a un pulso rectangular de amplitud unitaria de 120° (ciclo de trabajo 2/3) se obtiene el valor RMS (2/3) 1/2 = 0,8165.

Arroz. 14.7. Determinación de la raíz cuadrática media (RMS) para repetidos
impulsos
Es interesante comprobar este resultado sumando los armónicos correspondientes al mencionado tren de ondas cuadradas. En mesa. 14.2 muestra los resultados de esta suma. Como puedes ver, todo coincide.
Tabla 14.2. Los resultados de la sumatoria de armónicos correspondientes a
señal periódica con ciclo de trabajo 2/3 y amplitud unitaria
|
número armónico |
Amplitud armónica |
valores eficaces totales |
Con fines de comparación, cualquier conjunto de armónicos se puede agrupar y determinar el nivel general correspondiente de distorsión armónica. En este caso, el valor cuadrático medio de la señal está determinado por la fórmula
![]()
donde h\ es la amplitud del primer armónico (fundamental) y h„ es la amplitud de los armónicos de orden n > 1.
Los componentes responsables de la distorsión se pueden escribir por separado como
donde n > 1. Entonces
donde Fondo es el primer armónico y la distorsión armónica total (THD) es igual a D/Fondo.
Aunque el análisis de onda cuadrada es interesante, rara vez se usa en el mundo real. Los efectos de conmutación y otros procesos hacen que los pulsos rectangulares se parezcan más a los trapezoidales o, en el caso de los convertidores, con un flanco ascendente descrito por la expresión 1 cos(0) y un flanco descendente descrito por cos(0), donde 0< 0 en una escala logarítmica, la pendiente de las secciones correspondientes de este gráfico es -2 y -1.Para sistemas con valores típicos de reactancia, el cambio de pendiente ocurre aproximadamente en frecuencias del armónico 11 al 35 de la frecuencia de la red, y con una aumento en la reactancia o corriente en el sistema, la frecuencia de cambio de pendiente disminuye. El resultado práctico de todo esto es que los armónicos más altos son menos importantes de lo que uno podría pensar. Aunque aumentar la reactancia ayuda a reducir los armónicos de orden superior, esto no suele ser factible. Es más preferible reducir los componentes armónicos en la corriente consumida aumentando el número de pulsos durante la rectificación o conversión de voltaje, lograda por cambio de fase. Con respecto a los transformadores, este tema se tocó en el Cap. 7. Si el convertidor o rectificador de tiristores se alimenta de los devanados del transformador conectados en estrella y triángulo, y las salidas del convertidor o rectificador están conectadas en serie o en paralelo, se obtiene una rectificación de 12 pulsos. Los números armónicos del conjunto ahora son k = \2n ± 1 en lugar de k = 6u + 1, donde n es uno de los números enteros. En lugar de armónicos de 5º y 7º orden, ahora aparecen armónicos de 11º y 13º orden, cuya amplitud es mucho menor. Es bastante posible usar incluso más ondas y, por ejemplo, los sistemas de 48 pulsos se usan en grandes fuentes de alimentación para instalaciones electroquímicas. Dado que los grandes rectificadores y convertidores utilizan conjuntos de diodos o tiristores conectados en paralelo, el costo adicional de los devanados de cambio de fase en un transformador determina principalmente su precio. en la fig. 14.8 muestra las ventajas de un circuito de 12 pulsos sobre uno de 6 pulsos. Los armónicos de orden 11 y 13 en un circuito de 12 pulsos tienen un valor de amplitud típico de aproximadamente el 10% del primer armónico. En circuitos con gran número de ondulaciones, los armónicos son del orden k = pn + 1, donde p es el número de ondulaciones. Por interés, observamos que los pares de conjuntos armónicos que simplemente se desplazan entre sí 30° no se cancelan entre sí en un esquema de 6 pulsos. Estas corrientes armónicas fluyen de regreso a través del transformador; por lo tanto, se requiere un cambio de fase adicional para obtener la posibilidad de su aniquilación mutua. No todos los armónicos están en fase con el primero. Por ejemplo, en un conjunto armónico trifásico correspondiente a un tren de ondas cuadradas de 120°, las fases de los armónicos cambian según la secuencia -5, +7, -11, +13, etc. Cuando se desequilibra en un circuito trifásico, pueden presentarse componentes monofásicos, lo que conlleva una triplicación de armónicos con desfase cero. Arroz. 14.8. Espectros de 6 y 12 transductores de pulsaciones Los transformadores de aislamiento a menudo se consideran una panacea para los problemas de armónicos. Estos transformadores agregan algo de reactancia al sistema y, por lo tanto, ayudan a reducir los armónicos más altos; sin embargo, aparte de la supresión de corrientes de secuencia cero y el aislamiento electrostático, son de poca utilidad. Transformada de Fourier representa el medio más utilizado para convertir una función arbitraria de tiempo en un conjunto de sus componentes de frecuencia en el plano de números complejos. Esta transformación se puede aplicar a funciones aperiódicas para determinar sus espectros, en cuyo caso el operador complejo s se puede reemplazar con bigote: Para determinar las frecuencias más interesantes se puede utilizar la integración numérica en el plano complejo. Para familiarizarse con los conceptos básicos del comportamiento de estas integrales, consideramos varios ejemplos. en la fig. 14.6 (izquierda) muestra el pulso de área unitaria en el dominio del tiempo y su composición espectral; en el centro, un pulso de la misma área, pero de mayor amplitud, ya la derecha, la amplitud del pulso es infinita, pero su área sigue siendo igual a la unidad. La imagen de la derecha es especialmente interesante porque el espectro de pulsos de ancho cero contiene todas las frecuencias con amplitudes iguales. Arroz. 14.6.
En 1822 un matemático francés J. B. J. Fourier(J. B. J. Fourier) demostró en su trabajo sobre conductividad térmica que cualquier función periódica se puede descomponer en componentes iniciales, incluyendo una frecuencia de repetición y un conjunto de armónicos de esta frecuencia, cada uno de los cuales tiene su propia amplitud y fase con respecto a la tasa de repetición. . Las fórmulas básicas utilizadas en la transformada de Fourier son las siguientes: dónde L 0 es el componente DC, y PERO" y A"- armónicos de la frecuencia fundamental del orden PAGS, en fase y fase opuesta, respectivamente. Función f(x), por lo tanto, es la suma de estos armónicos y /1 0 . En los casos en que /(.r) es simétrico con respecto a n/2, es decir, /(x) en la región de n a 2n = -/(x) en la región de 0 a n, y no hay componente de corriente continua , las fórmulas de Fourier -transformaciones se simplifican a: dónde PAGS - 1,3,5, 7.... Todos los armónicos son sinusoides, solo algunos de ellos están en fase y algunos están desfasados con la frecuencia fundamental. La mayoría de las formas de onda que se encuentran en la electrónica de potencia se pueden descomponer en armónicos de esta manera. Si se aplica la transformada de Fourier a pulsos rectangulares con una duración de 120°, entonces los armónicos formarán un conjunto de orden k = 6p± 1, donde PAGS es uno de los enteros. Amplitud de cada armónico h en relación con el primero está relacionado con su número por la razón h = /k. En este caso, el primer armónico tendrá una amplitud 1,1 veces mayor que la amplitud de una señal rectangular. La transformada de Fourier da el valor de amplitud de cada armónico, pero como todos son sinusoidales, el valor rms se obtiene simplemente dividiendo la amplitud correspondiente por la raíz de 2. El valor rms de una señal compleja es la raíz cuadrada de la suma de los cuadrados de los valores rms de cada armónico, incluido el primero. Cuando se trata de funciones de impulsos repetitivos, es útil considerar el ciclo de trabajo. Si los pulsos repetidos en la Fig. 14.7 son RMS X durante PERO, entonces el valor de la raíz cuadrática media para el tiempo A será igual a alto (largo/ancho) ( 2. Por lo tanto, el valor RMS de los pulsos repetitivos es proporcional a la raíz cuadrada del valor del ciclo de trabajo. Aplicando este principio a un pulso rectangular de 120° (ciclo de trabajo 2/3) con amplitud unitaria, obtenemos el valor RMS (2/3) 12 = 0.8165. Arroz. 14.7.
impulsos Es interesante comprobar este resultado sumando los armónicos correspondientes al mencionado tren de ondas cuadradas. En mesa. 14.2 muestra los resultados de esta suma. Como puedes ver, todo coincide. Tabla 14.2. Los resultados de la sumatoria de armónicos correspondientes a señal periódica con ciclo de trabajo 2/3 y amplitud unitaria Con fines de comparación, cualquier conjunto de armónicos se puede agrupar y determinar el nivel general correspondiente de distorsión armónica. En este caso, el valor cuadrático medio de la señal está determinado por la fórmula dónde h- amplitud del primer armónico (fundamental), a h „- amplitud de armónicos de orden PAGS > 1. Los componentes responsables de la distorsión se pueden escribir por separado como dónde n> 1. Entonces dónde fondo- primer armónico y THD(THD) será igual a D/fondo. Aunque el análisis de onda cuadrada es interesante, rara vez se usa en el mundo real. Los efectos de conmutación y otros procesos hacen que los pulsos rectangulares se parezcan más a los trapezoidales o, en el caso de los convertidores, con un flanco ascendente descrito por la expresión 1 - cos(0) y un flanco descendente descrito por la relación cos(0), donde 0 Incremento en Los tiempos de subida y bajada de la onda cuadrada "suavizan" el conjunto de armónicos correspondientes, de modo que la amplitud de los armónicos de alto orden disminuye en proporción a (1/Ar) en lugar de (1 /a) a frecuencias más bajas. Al mostrar la dependencia de estas amplitudes de la frecuencia en papel con una escala logarítmica doble, la pendiente de las secciones correspondientes de este gráfico es -2 y -1. A medida que aumenta la reactancia o corriente en el sistema, la frecuencia del cambio de pendiente disminuye. . El resultado práctico de todo esto es que los armónicos más altos son menos importantes de lo que uno podría pensar. Aunque el aumento resistencia reactiva contribuye a la reducción de armónicos de orden superior, esto generalmente no es factible. Más preferido para reducción de componentes armónicos en la corriente consumida es el aumento en el número de pulsos durante la rectificación o conversión de voltaje, logrado por cambio de fase. Con respecto a los transformadores, este tema se tocó en el Cap. 7. Si el convertidor o rectificador de tiristores se alimenta de los devanados del transformador conectados en estrella y triángulo, y las salidas del convertidor o rectificador están conectadas en serie o en paralelo, se obtiene una rectificación de 12 nulos. Ahora se obtienen los números armónicos en un conjunto k = 12PAGS± 1 en su lugar k = 6w ± 1, donde PAGS es uno de los enteros. En lugar de los armónicos de 5º y 7º orden, ahora aparecen armónicos de 11º y 13º orden, cuya amplitud es mucho menor. Es bastante posible usar incluso más pulsaciones y, por ejemplo, en grandes fuentes de alimentación para instalaciones electroquímicas, se usan sistemas de 48 pulsaciones. Dado que los grandes rectificadores y convertidores utilizan conjuntos de diodos o tiristores conectados en paralelo, el costo adicional de los devanados de cambio de fase en un transformador determina principalmente su precio. en la fig. 14.8 muestra las ventajas de un circuito de 12 pulsos sobre uno de 6 pulsaciones. Los armónicos de orden 11 y 13 en el circuito de 12 nulos tienen un valor de amplitud típico de aproximadamente el 10% del primer armónico. En circuitos con gran número de ondulaciones, los armónicos son del orden k = págs.± 1, donde R- número de pulsaciones. En aras del interés, tenga en cuenta que los pares de conjuntos armónicos que simplemente se desplazan entre sí en 30° no se cancelan entre sí en un circuito de 6 pulsos. Estas corrientes armónicas fluyen de regreso a través del transformador; por lo tanto, se requiere un cambio de fase adicional para obtener la posibilidad de su aniquilación mutua. No todos los armónicos están en fase con el primero. Por ejemplo, en un conjunto armónico trifásico correspondiente a un tren de onda cuadrada de 120°, las fases de los armónicos cambian según la secuencia -5, +7, -11, +13, etc. Cuando se desequilibra en un trifásico Pueden producirse componentes monofásicos del circuito, lo que conlleva una triplicación de armónicos con desfase nulo. Arroz. 14.8.
Transformadores de aislamiento a menudo visto como una panacea para problemas armónicos. Estos transformadores agregan algo de reactancia al sistema y, por lo tanto, ayudan a reducir los armónicos más altos; sin embargo, aparte de la supresión de corrientes de secuencia cero y el aislamiento electrostático, son de poca utilidad. Casi cualquier función periódica se puede descomponer en armónicos simples utilizando una serie trigonométrica (serie de Fourier): F(X) = + (un porque nx + segundo norte pecado nx), (*) Escribimos esta serie como una suma de armónicos simples, asumiendo que los coeficientes son iguales un= Un pecado jn, segundo norte= Un porque jn. Obtenemos: un porque jn + segundo norte pecado jn = Un pecado( nx+ jn), dónde Un= , tg jn = . (**) Entonces la serie (*) en forma de armónicos simples toma la forma F(X) = La serie de Fourier representa una función periódica como la suma de un número infinito de sinusoides, pero con frecuencias que tienen un cierto valor discreto. Algunas veces norte El armónico se escribe como un porque nx + segundo norte pecado nx = Un porque nx – jn) , dónde un= Un porque jn , segundo norte= Un pecado jn . Donde Un y jn están determinados por las fórmulas (**). Entonces la serie (*) tomará la forma F(X) = Definición 9. Operación de representación de función periódica F(X) junto a Fourier se llama análisis armónico. La expresión (*) también se encuentra en otra forma más común: Posibilidades un, segundo norte están determinados por las fórmulas: magnitud C 0 expresa el valor promedio de la función durante el período y se denomina componente constante, que se calcula mediante la fórmula: En la teoría de oscilaciones y análisis espectral, la representación de la función F(t) en una serie de Fourier se escribe como: aquellos. la función periódica está representada por la suma de los términos, cada uno de los cuales es una oscilación sinusoidal con una amplitud C norte y fase inicial jn, es decir, la serie de Fourier de una función periódica consta de armónicos individuales con frecuencias que difieren entre sí por un número constante. Además, cada armónico tiene una cierta amplitud. Valores C norte y jn deben elegirse correctamente para que se cumpla la igualdad (***), es decir, están determinados por las fórmulas (**) [ C norte = Un]. Reescribamos la serie de Fourier (***) como Definición 10. Conjunto de cantidades C norte, es decir, la dependencia de la amplitud de la frecuencia, se llama espectro de amplitud de la función o espectro de amplitud. Definición 11. Conjunto de cantidades jn se llama espectro de fase. Cuando dicen simplemente “espectro”, se refieren exactamente al espectro de amplitud, en otros casos hacen las reservas correspondientes. La función periódica tiene espectro discreto(es decir, se puede representar como armónicos individuales). El espectro de una función periódica se puede representar gráficamente. Para ello elegimos las coordenadas C norte y w = noroeste una . El espectro se representará en este sistema de coordenadas mediante un conjunto de puntos discretos, ya que cada valor noroeste 1 corresponde a un valor específico Con n. Un gráfico que consta de puntos individuales es inconveniente. Por lo tanto, es habitual representar las amplitudes de los armónicos individuales como segmentos verticales de la longitud adecuada (Fig. 2). Este espectro discreto a menudo se denomina espectro de línea. Es un espectro armónico, es decir consta de líneas espectrales igualmente espaciadas; las frecuencias armónicas están en proporciones múltiples simples. Los armónicos separados, incluido el primero, pueden estar ausentes, es decir, sus amplitudes pueden ser iguales a cero, pero esto no viola la armonía del espectro. Los espectros discretos o lineales pueden pertenecer tanto a funciones periódicas como no periódicas. En el primer caso, el espectro es necesariamente armónico. La expansión de la serie de Fourier se puede generalizar al caso de una función no periódica. Para ello, debemos aplicar el paso al límite como T®∞, considerando una función no periódica como el caso límite de una función periódica de periodo indefinidamente creciente. en lugar de 1/ T introducir la frecuencia fundamental circular w 1 = 2p/ T. Este valor es el intervalo de frecuencia entre armónicos adyacentes, cuyas frecuencias son iguales a 2p norte/T. si un T® ∞, entonces w 1® dw y 2p norte/T® w, dónde w es la frecuencia actual, que cambia continuamente, dw- su incremento. En este caso, la serie de Fourier se convertirá en la integral de Fourier, que es la expansión de una función no periódica en un intervalo infinito (–∞;∞) en oscilaciones armónicas, cuyas frecuencias w cambiar continuamente de 0 a ∞: Una función no periódica tiene un espectro continuo o continuo, es decir en lugar de puntos individuales, el espectro se representa como una curva continua. Esto se obtiene como resultado de pasar al límite de la serie a la integral de Fourier: los intervalos entre las líneas espectrales individuales disminuyen indefinidamente, las líneas se fusionan y en lugar de puntos discretos, el espectro se representa mediante una secuencia continua de puntos, es decir. curva continua. Funciones a(w) y b(w) dar la ley de distribución de amplitudes y fases iniciales en función de la frecuencia w. Descomposición de funciones periódicas no sinusoidales Definiciones generales Parte 1. Teoría de circuitos lineales (continuación) INGENIERIA ELÉCTRICA BASES TEÓRICAS Libro de texto para estudiantes de especialidades de energía eléctrica. T. Circuitos eléctricos de corriente periódica no senoidal Como sabe, en la industria de la energía eléctrica, se adopta una forma sinusoidal como forma estándar para corrientes y voltajes. Sin embargo, en condiciones reales, las formas de las curvas de corrientes y tensiones pueden diferir en cierta medida de las sinusoidales. Las distorsiones en las formas de las curvas de estas funciones en los receptores conducen a pérdidas de energía adicionales y a una disminución de su eficiencia. La forma sinusoidal de la curva de voltaje del generador es uno de los indicadores de la calidad de la energía eléctrica como mercancía. Son posibles las siguientes razones para la distorsión de la forma de las curvas de corrientes y voltajes en un circuito complejo: 1) la presencia en el circuito eléctrico de elementos no lineales, cuyos parámetros dependen de los valores instantáneos de corriente y voltaje [ R, L, C=f(tu, yo)], (por ejemplo, rectificadores, unidades de soldadura eléctrica, etc.); 2) la presencia en el circuito eléctrico de elementos paramétricos, cuyos parámetros cambian con el tiempo [ R, L, C=f(t)]; 3) la fuente de energía eléctrica (generador trifásico), debido a las características de diseño, no puede proporcionar una forma sinusoidal ideal del voltaje de salida; 4) influencia en el complejo de los factores enumerados anteriormente. Los circuitos no lineales y paramétricos se analizan en capítulos separados del curso TOE. Este capítulo investiga el comportamiento de los circuitos eléctricos lineales cuando se exponen a fuentes de energía con una forma de onda no sinusoidal. Se sabe por el curso de las matemáticas que cualquier función periódica del tiempo F(t) que satisface las condiciones de Dirichlet se puede representar mediante la serie armónica de Fourier: Aquí PERO 0 - componente constante, - k-th componente armónico o abreviado k Soy una armónica. El primer armónico se llama fundamental, y todos los armónicos posteriores se llaman los más altos. Amplitudes de armónicos individuales A a no depende de la forma en que se expande la función F(t) en una serie de Fourier, mientras que las fases iniciales de los armónicos individuales dependen de la elección de la referencia de tiempo (origen). Los armónicos individuales de la serie de Fourier se pueden representar como la suma de los componentes del seno y el coseno: Entonces toda la serie de Fourier tomará la forma: Las relaciones entre los coeficientes de las dos formas de la serie de Fourier son: si un k El armónico y sus componentes seno y coseno se reemplazan por números complejos, entonces la relación entre los coeficientes de la serie de Fourier se puede representar en forma compleja: Si una función de tiempo periódica no sinusoidal se da (o se puede expresar) analíticamente en forma de ecuación matemática, entonces los coeficientes de la serie de Fourier se determinan mediante las fórmulas conocidas en el curso de las matemáticas: En la práctica, la función no sinusoidal investigada F(t) generalmente se establece en forma de diagrama gráfico (gráficamente) (Fig. 118) o en forma de tabla de coordenadas de puntos (tabular) en el intervalo de un período (Tabla 1). Para realizar un análisis armónico de tal función de acuerdo con las ecuaciones anteriores, primero debe ser reemplazada por una expresión matemática. Reemplazar una función dada de forma gráfica o tabular por una ecuación matemática se denomina aproximación de función.




![]()

![]()

![]() .
.![]() .
.


![]() (***)
(***)![]() dónde w 1 es la frecuencia principal. De esto podemos concluir: una función periódica compleja F(t) está determinada por el conjunto de cantidades C norte y jn .
dónde w 1 es la frecuencia principal. De esto podemos concluir: una función periódica compleja F(t) está determinada por el conjunto de cantidades C norte y jn . Arroz. 2.
Arroz. 2.